
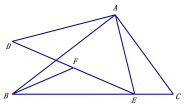
【题目】如图,△ABC∽△ADE,∠BAC =∠ADE =90°,AB=4,AC=3,F是DE的中点,若点E是直线BC上的动点,连接BF,则BF的最小值是_______.
【答案】2
【解析】
连接DB,先求出∠DBE=90°,F是DE的中点,可得BF=![]() DE,再根据当AE⊥BC时,AE最短,此时DE最短,根据直角三角形的面积以及相似三角形的性质,求得DE的最小值,即可得出BF的最小值.
DE,再根据当AE⊥BC时,AE最短,此时DE最短,根据直角三角形的面积以及相似三角形的性质,求得DE的最小值,即可得出BF的最小值.
如图,连接DB,

∵∠BAC =90°,AB=4,AC=3,
∴BC=5,
∵△ABC∽△ADE,
∴∠ADE=∠ABC,
又∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴![]() ,
,
又∵∠AOE=∠DOB,
∴△AOE∽△DOB,
∴∠DBO=∠AEO,
又∵Rt△ADE中,∠ADE+∠AEO=90![]() ,又∠ADE=∠ABC,
,又∠ADE=∠ABC,
∴∠DBO +∠ABC =90![]() ,即∠DBE=90
,即∠DBE=90![]() ,
,
∵F是DE的中点,
∴BF=![]() DE,
DE,
∵△ABC∽△ADE,
∴当AE⊥BC时,AE最短,此时DE最短,
当AE⊥BC时,AE=![]() =
=![]() ,
,
∵△ABC∽△ADE,
∴![]() ,即3DE=
,即3DE=![]() ,
,
∴DE=4,
∴BF=![]() ×4=2.
×4=2.
故答案为:2.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
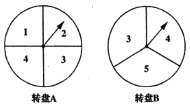
【题目】甲、乙两人在玩转盘游戏时,把两个可以自由传动的转盘A,B分别分成4等份,3等份的扇形区域,并在每一小区域内标上数字(如图所示).游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为奇数,则甲胜;若指针所指两个区域的数字之和为偶数,则乙胜.如果指针落在分割线上,则需要重新转动转盘.请问这个游戏规则对甲、乙双方公平吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下框中是小明对一道题目的解答以及老师的批改.
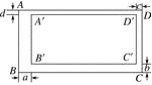
题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2∶1,在温室内,沿前侧内墙保留3 m的空地,其他三侧内墙各保留1 m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288 m2?

解:设矩形蔬菜种植区域的宽为x_m,则长为2xm,
根据题意,得x·2x=288.
解这个方程,得x1=-12(不合题意,舍去),x2=12,
所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)
答:当温室的长为28 m,宽为14 m时,矩形蔬菜种植区域的面积是288 m2.
我的结果也正确!
小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.
结果为何正确呢?
(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样?
(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD∶AB=2∶1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
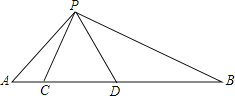
【题目】如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
(1)求∠APB的大小.
(2)说明线段AC、CD、BD之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
(1)古希腊著名数学家欧几里得在《几何原本》提出了射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项.射影定理是数学图形计算的重要定理.
其符号语言是:如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则:(1)CD = AD·BD, (2)AC = AB·AD, (3)BC=AB·BD;请你证明定理中的结论(2)BC=AB·BD.
(结论运用)
(2)如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
①求证:△BOF∽△BED;
②若![]() ,求OF的长.
,求OF的长.
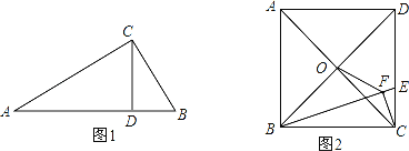
查看答案和解析>>
科目:初中数学 来源: 题型:
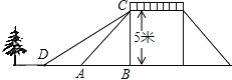
【题目】如图,某公园内有座桥,桥的高度是5米,CB⊥DB,坡面AC的倾斜角为45°,为方便老人过桥,市政部门决定降低坡度,使新坡面DC的坡度为i= ![]() :3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据:
:3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
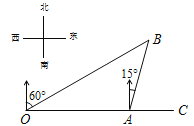
【题目】如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的解答过程,求y2+4y+8的最小值.解:y2+4y+8=y2+4y+4+4-(y+2)2+4,∵(y+2)2≥0,∴(y+2)2+4≥4,∴y2+4y+8的最小值为4.仿照上面的解答过程,求x2-x+4的最小值和6-2x-x2的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com