
���� ����ʮ����˷����䷽����ƽ���ʽ�����ݷǸ��������ʽ�ɣ�
��� �⣺��1��m2-6m+8=m2-6m+9-1=��m-3��2-1=��m-2����m-4����
��2��x2+4x+5=x2+4x+4+1=��x+2��2+1��
�ߣ�x+2��2��0��
�ࣨx+2��2+1��1��
�����ʽx2+4x+5����Сֵ1��
��3��x2+y2-4x+6y+18=x2-4x+4+y2+6y+9+5=��x-2��2+��y+3��2+5��
�൱x=2��y=-3ʱ������ʽx2+y2-4x+6y+18����Сֵ�������Сֵ��5��
���� ���⿼�������ʽ�ֽ��Ӧ�ã����շǸ��������ʡ�ʮ����˷���ʽ�ֽ��ǽ���Ĺؼ���


 ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
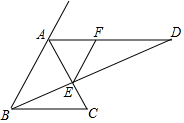 ��ͼ���ڡ�ABC�У�AB=AC��BEƽ�֡�ABC��AD��BC��AD��BE���ӳ�����D��EFƽ�֡�AED����AB=8��AF=3��AE��ED=AF��FD����CE=$\frac{7}{2}$��
��ͼ���ڡ�ABC�У�AB=AC��BEƽ�֡�ABC��AD��BC��AD��BE���ӳ�����D��EFƽ�֡�AED����AB=8��AF=3��AE��ED=AF��FD����CE=$\frac{7}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com