
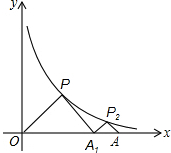
 如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )
如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )| A. | (4,0) | B. | (4$\sqrt{2}$,0) | C. | (2,0) | D. | (2$\sqrt{2}$,0) |
分析 过P作PB⊥x轴于B,根据等腰直角三角形的性质得到BP=BO=BA1,设OB=a,则P点坐标为(a,a),把它代入y=$\frac{4}{x}$(x>0)可求得a的值,而OA1=2a,从而确定A点坐标;同理可设P2(a+b,b),求出b的值即可得出结论.
解答 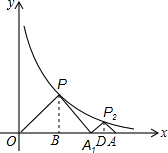 解:过P作PB⊥x轴于B,如图
解:过P作PB⊥x轴于B,如图
∵△POA是等腰直角三角形,
∴BP=BO=BA,
设OB=a,则P点坐标为(a,a),
∵点P在函数y=$\frac{4}{x}$(x>0)的图象上,
∴a2=4,
∴a=2,
∴OA=2a=4,
∴A点坐标为(4,0).
设P2(4+b,b),则b(4+b)=4,解得b1=-2-2$\sqrt{2}$(舍去),b2=-2+2$\sqrt{2}$,
∴AA1=2b=-4+4$\sqrt{2}$,
∴OA=4-4+4$\sqrt{2}$=4$\sqrt{2}$,
∴A(4$\sqrt{2}$,0).
故选B.
点评 本题考查了点在反比例函数图象上,则点的横纵坐标满足反比例的解析式.也考查了等腰直角三角形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若$\frac{CF}{BF}$=$\frac{2}{3}$,$\frac{AG}{GE}$=$\frac{2}{1}$,求$\frac{{S}_{△DGE}}{{S}_{△ADC}}$.
如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若$\frac{CF}{BF}$=$\frac{2}{3}$,$\frac{AG}{GE}$=$\frac{2}{1}$,求$\frac{{S}_{△DGE}}{{S}_{△ADC}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{7}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2x+1}$ | B. | $\frac{1}{2x-1}$ | C. | $\frac{1-3x}{{x}^{2}}$ | D. | $\frac{5x+3}{2{x}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 312×104 | B. | 0.312×107 | C. | 3.12×106 | D. | 3.12×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | 3 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)
某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
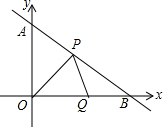 综合与探究:如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.
综合与探究:如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com