
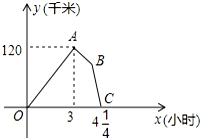
 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,则快递车从乙地返回时的速度为90千米/时.
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,则快递车从乙地返回时的速度为90千米/时. 分析 设快递车从甲地到乙地的速度为x千米/时,根据3小时相距120千米即可列方程求解,根据条件AB段所用的时间是45分钟,利用甲和乙之间的距离减去货车行驶的距离即可求得B点对应的横坐标,设快递车从乙地返回甲地的速度是y千米/小时,根据距离公式即可列方程求解.
解答 解:设快递车从甲地到乙地的速度为x千米/时,则
3(x-60)=120,
x=100.
则甲、乙两地之间的距离是3×100=300(千米);
快递车返回时距离货车的距离是:300-60(3+$\frac{45}{60}$)=75(千米),
设快递车从乙地返回甲地的速度是y千米/小时.
根据题意得:(60+y)【4$\frac{1}{4}$-(3+$\frac{45}{60}$)】=75,
解得:y=90.
则快递车从乙地返回甲地的速度是90千米/小时.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题,关键是根据一次函数的性质和图象结合实际问题求解.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>5或a<-2 | B. | -2≤a≤5 | C. | -2<a<5 | D. | a≥5或a≤-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运往地 车 型 | 甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 720 | 800 |
| 小货车 | 500 | 650 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰三角形DEF中,DE=FE=1,∠DEF=135°.
如图,在等腰三角形DEF中,DE=FE=1,∠DEF=135°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
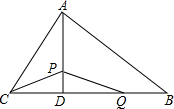 如图,在△ABC中,高AD交边BC于点D,AD=12cm,BD=16cm,CD=8cm.动点P从点D出发,沿折线D-A-B向终点B运动,点P在AD上的速度4cm/s,在AB上的速度5cm/s.同时点Q从点B出发,以6cm/s的速度,沿BC向终点C运动,当点Q停止运动时,点P也随之停止.设点P的运动时间为t(s).
如图,在△ABC中,高AD交边BC于点D,AD=12cm,BD=16cm,CD=8cm.动点P从点D出发,沿折线D-A-B向终点B运动,点P在AD上的速度4cm/s,在AB上的速度5cm/s.同时点Q从点B出发,以6cm/s的速度,沿BC向终点C运动,当点Q停止运动时,点P也随之停止.设点P的运动时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com