
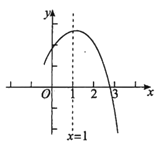
【题目】如图是二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )图象的一部分,与
)图象的一部分,与![]() 轴的交点
轴的交点![]() 在点
在点![]() 和
和![]() 之间,对称轴是
之间,对称轴是![]() .有下列说法:①
.有下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤当
为实数);⑤当![]() 时,
时,![]() .其中正确的是______(填写所有正确结论的序号).
.其中正确的是______(填写所有正确结论的序号).
【答案】①②④
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴判定b与0的关系以及2a+b=0;当x=-1时,y=a-b+c;然后由图象确定当x取何值时,y>0.
解:①∵对称轴在y轴右侧,
∴a、b异号,
∴ab<0,故正确;
②∵对称轴x=-![]() =1,
=1,
∴2a+b=0;故正确;
③∵2a+b=0,
∴b=-2a,
∵当x=-1时,y=a-b+c<0,
∴a-(-2a)+c=3a+c<0,故错误;
④根据图象知,当m=1时,有最大值;
当m≠1时,有am2+bm+c≤a+b+c,
所以a+b≥m(am+b)(m为实数).故正确.
⑤如图,当-1<x<3时,y不只是大于0.故错误.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】小明的书包里只放了A4大小的试卷共4张,其中语文1张、数学2张、英语1张
![]() 若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
![]() 若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)试求抛物线的解析式;
(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=![]() ,试求m的最大值及此时点P的坐标;
,试求m的最大值及此时点P的坐标;
(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Q是弧AB与弦AB所围成的图形的内部的一定点,P是弦AB上一动点,连接PQ并延长交弧AB于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,A,C两点间的距离为y2cm.
小明根据学习函数的经验,分别对函数y1,y2,随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)确定自变量x的取值范围是 .
(2)按下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值.
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.62 | 4.67 | 3.76 | 2.65 | 3.18 | 4.37 | |
y2/cm | 5.62 | 5.59 | 5.53 | 5.42 | 5.19 | 4.73 | 4.11 |
(3)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并面出函数y1,y2的图象.
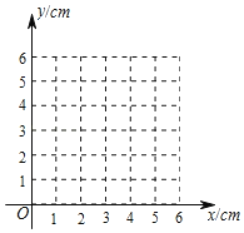
(4)结合函数图象,解决问题:当△APC为等腰三角形时,AP的长度约为 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
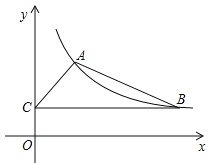
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A,B,C三种货车若干辆,A,B,C每辆货车的日运货量之比为1:2:3,为应对双11物流高峰,该公司重新调配了这三种货车的数量,调配后,B货车数量增加一倍,A,C货车数量各减少50%,三种货车日运货总量增加25%,按调配后的运力,三种货车在本地运完一堆货物需要t天,但A,C两种货车运了若干天后全部被派往外地执行其它任务,剩下的货物由B货车运完,运输总时间比原计划多了4天,且B货车运输时间刚好为A,C两种货车在本地运输时间的6倍,则B货车共运了______天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数y=![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 函数图象分别位于第一、第三象限
B. 当x>0时,y随x的增大而减小
C. 函数图象经过点(1,2)
D. 若点A(x1,y1),B(x2,y2)都在函数图象上,且x1<x2,则y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.
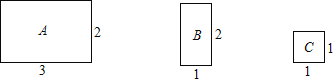
(1)搅匀后从中摸出1个盒子,求摸出的盒子中是![]() 型矩形纸片的概率;
型矩形纸片的概率;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的两个盒子中摸出一个盒子,求2次摸出的盒子的纸片能拼成一个新矩形的概率(不重叠无缝隙拼接).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com