
 如图,已知在△ABC中,∠ABC=90°,点E是AC的中点,联结BE,过点C作CD∥BE,且∠ADC=90°,在DC取点F,使DF=BE,分别联结BD、EF.
如图,已知在△ABC中,∠ABC=90°,点E是AC的中点,联结BE,过点C作CD∥BE,且∠ADC=90°,在DC取点F,使DF=BE,分别联结BD、EF.分析 (1)根据直角三角形斜边上的中线的性质求出BE=DE,根据等腰三角形性质求出即可;
(2)证出DE=DF,得出∠DEF=∠DFE,证出∠BEF=∠DEF,即可得出结论.
解答 (1)证明:∵∠ABC=90°,∠ADC=90°,点E是AC的中点,
∴$BE=\frac{1}{2}AC$,$DE=\frac{1}{2}AC$.(直角三角形斜边上的中线等于斜边的一半)
∴BE=DE.
(2)证明:∵CD∥BE,
∴∠BEF=∠DFE.
∵DF=BE,BE=DE,
∴DE=DF.
∴∠DEF=∠DFE.
∴∠BEF=∠DEF.
∴EF垂直平分BD.(等腰三角形三线合一)
点评 本题主要考查对直角三角形斜边上中线的性质,等腰三角形性质等知识点的理解和掌握,能求出BE=DE是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
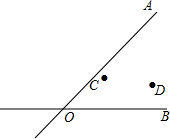 在加快城镇建设中,有两条公路OA和OB交汇于O点,在图中∠AOB的内部有蔬菜基地C和D,现要修建一个蔬菜转运站P,使转运站P到两条公路OA、OB的距离相等,且到两个蔬菜基地C、D的距离相等,用尺规作出蔬菜转运站P的位置.(要求:不写作法,保留作图痕迹.)
在加快城镇建设中,有两条公路OA和OB交汇于O点,在图中∠AOB的内部有蔬菜基地C和D,现要修建一个蔬菜转运站P,使转运站P到两条公路OA、OB的距离相等,且到两个蔬菜基地C、D的距离相等,用尺规作出蔬菜转运站P的位置.(要求:不写作法,保留作图痕迹.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,C,D是⊙O上的两点(在直径AB的同一侧),且$\widehat{BC}$=$\widehat{CD}$,弦AC、BD相交于点P,如果∠APB=110°,求∠ABD的度数.
如图,AB是⊙O的直径,C,D是⊙O上的两点(在直径AB的同一侧),且$\widehat{BC}$=$\widehat{CD}$,弦AC、BD相交于点P,如果∠APB=110°,求∠ABD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2016年全国中小学生“安全教育日”主题:“强化安全意识,提升安全素养”,小刚骑单车上学,当他骑了一段,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校.以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
2016年全国中小学生“安全教育日”主题:“强化安全意识,提升安全素养”,小刚骑单车上学,当他骑了一段,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校.以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com