
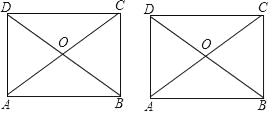
【题目】如图,已知矩形ABCD,AB=6,AD=2![]() ,对角线AC,BD交于点O,E为对角线AC上一点.
,对角线AC,BD交于点O,E为对角线AC上一点.
(1)求证:△OBC是等边三角形;
(2)连结BE,当BE=![]() 时,求线段AE的长;
时,求线段AE的长;
(3)在BC边上取点F,设P,Q分别为线段AE,BF的中点,连结EF,PQ.若EF=2,求PQ的取值范围.
【答案】(1)详见解析;(2)当BE=![]() 时,线段AE的长为3
时,线段AE的长为3![]() ﹣1或3
﹣1或3![]() +1;(3)PQ的取值范围为
+1;(3)PQ的取值范围为![]() ≤PQ≤4.
≤PQ≤4.
【解析】
(1)根据矩形的性质可得:AD=BC=2![]() ,OA=OC=OB=OD,∠ABC=90°,然后利用勾股定理即可求出AC,从而求出OB、OC,即可证出△OBC是等边三角形;
,OA=OC=OB=OD,∠ABC=90°,然后利用勾股定理即可求出AC,从而求出OB、OC,即可证出△OBC是等边三角形;
(2)作BM⊥AC于M,先求出∠BAC,根据锐角三角函数,即可分别求出BM和AM,根据勾股定理即可求出EM,最后根据点E的位置分类讨论,即可求出AE的值;
(3)作EG⊥BC于G,作PN⊥BC于N,则EG![]() PN
PN![]() AB,易知PN为梯形EABG的中位线,点N为BG的中点,设EG=x,根据题意,先求出x的取值范围,然后根据梯形中位线的性质和勾股定理分别求出PN和FG,从而求出QN,再根据勾股定理求出
AB,易知PN为梯形EABG的中位线,点N为BG的中点,设EG=x,根据题意,先求出x的取值范围,然后根据梯形中位线的性质和勾股定理分别求出PN和FG,从而求出QN,再根据勾股定理求出![]() 与x的函数关系式,根据一次函数的增减性即可求出
与x的函数关系式,根据一次函数的增减性即可求出![]() 的最值,从而求出PQ的取值范围.
的最值,从而求出PQ的取值范围.
(1)证明:∵四边形ABCD是矩形,
∴AD=BC=2![]() ,OA=OC=OB=OD,∠ABC=90°
,OA=OC=OB=OD,∠ABC=90°
∴AC=![]() =
=![]() =4
=4![]() ,
,
∴OB=OC=2![]() ,
,
∴OB=OC=BC,
∴△OBC是等边三角形;
(2)解:作BM⊥AC于M,如图1所示:
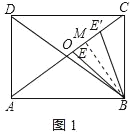
∵△OBC是等边三角形,
∴∠ACB=60°,
∴∠BAC=30°,
∴BM=![]() AB=3,
AB=3,
∴AM=![]() BM=3
BM=3![]() ,EM=
,EM=![]() =
=![]() =1,
=1,
当点E在M的左侧时,AE=AM﹣EM=3![]() ﹣1;
﹣1;
当点E在M的右侧时,AE=AM+EM=3![]() +1;
+1;
综上所述,当BE=![]() 时,线段AE的长为3
时,线段AE的长为3![]() ﹣1或3
﹣1或3![]() +1;
+1;
(3)解:作EG⊥BC于G,作PN⊥BC于N,则EG![]() PN
PN![]() AB,
AB,
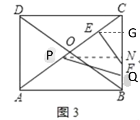
易知PN为梯形EABG的中位线,点N为BG的中点
设EG=x,当点E与C重合时,EG的最小值为0;如图所示EG≤EF=2,即0≤x≤2
∴PN=![]() (EG+AB)=
(EG+AB)=![]() ,根据勾股定理:FG=
,根据勾股定理:FG=![]()
∵点Q、N分别为BF、BG的中点
∴BQ=![]() BF,BN=
BF,BN=![]() BG
BG
∴QN= BN-BQ=![]() BG-
BG-![]() BF=
BF=![]() (BG-BF)=
(BG-BF)=![]() FG=
FG=![]() ,
,
∴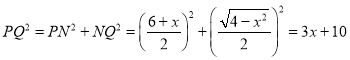
∵3>0
∴![]() 随x的增大而增大
随x的增大而增大
∴当x=0时,![]() 的最小值为10,当x=2时,
的最小值为10,当x=2时,![]() 的最大值为16
的最大值为16
∴PQ的取值范围为![]() ≤PQ≤4.
≤PQ≤4.


科目:初中数学 来源: 题型:
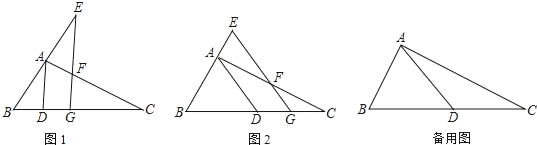
【题目】如图,Rt△ABC中,∠BAC=90°,AB=2,AC=4,D是BC边上一动点,G是BC边上的一动点,GE∥AD分别交AC、BA或其延长线于F、E两点
(1)如图1,当BC=5BD时,求证:EG⊥BC;
(2)如图2,当BD=CD时,FG+EG是否发生变化?证明你的结论;
(3)当BD=CD,FG=2EF时,DG的值= .
查看答案和解析>>
科目:初中数学 来源: 题型:
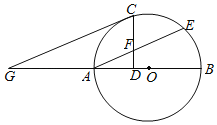
【题目】如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.
(1)求证:CG是⊙O的切线.
(2)求证:AF=CF.
(3)若sinG=0.6,CF=4,求GA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=10,高AD=8,M、N、P分别在边AB、BC、AC上移动,但不与A、B、C重合,连接MN、NP、MP,且MP始终与BC保持平行,AD与MP相交于点E,设MP=x,△MNP的面积用y表示.
(1)求y关于x的函数关系式;
(2)当x取什么值时,y有最大值,并求出的最大值;
(3)当x取什么值时,△MNP是等腰直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
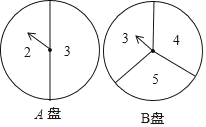
【题目】甲、乙两同学玩转盘游戏时,把质地相同的两个盘A、B分别平均分成2份和3份,并在每一份内标有数字如图.游戏规则:甲、乙两同学分别同时转动两个转盘各1次,当转盘停止后,指针所在区域的数字之积为偶数时甲胜;数字之积为奇数时乙胜.若指针恰好在分割线上,则需要重新转动转盘.
(1)用树状图或列表的方法,求甲获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
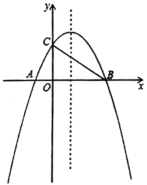
【题目】如图,抛物线![]() 与x轴交与A(1,0),B(- 3,0)两点
与x轴交与A(1,0),B(- 3,0)两点
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求该抛物线的函数表达式;
(2)若点![]() 为抛物线对称轴上一点,抛物线上是否存在点
为抛物线对称轴上一点,抛物线上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点
为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)点![]() 是直线
是直线![]() 上方抛物线上的点,若
上方抛物线上的点,若![]() ,求出
,求出![]() 点的到
点的到![]() 轴的距离.
轴的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图中的![]() 型(正方形)、
型(正方形)、![]() 型(菱形)、
型(菱形)、![]() 型(等腰直角三角形)纸片分别放在
型(等腰直角三角形)纸片分别放在![]() 个盒子中,盒子的形状、大小、质地都相同,再将这
个盒子中,盒子的形状、大小、质地都相同,再将这![]() 个盒子装入一只不透明的袋子中.
个盒子装入一只不透明的袋子中.
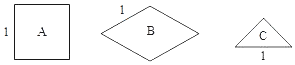
(1)搅匀后从中摸出![]() 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
(2)搅匀后先从中摸出![]() 个盒子(不放回),再从余下的
个盒子(不放回),再从余下的![]() 个盒子中摸出
个盒子中摸出![]() 个盒子,把摸出的
个盒子,把摸出的![]() 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c经过点A(﹣1,0),与y轴交于点B,且对称轴为x=1.
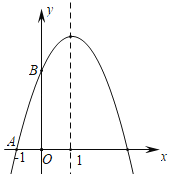
(1)求该抛物线的解析式;
(2)点P是抛物线对称轴上的一动点,当|PA﹣PB|取最大值时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com