
����Ŀ����һ�ž���ֽƬABCD�����۵�������������£�
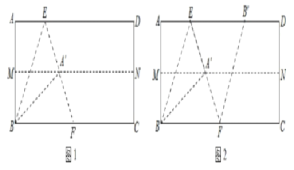
��һ�����ȶ��ۣ�ʹAD��BC�غϣ��õ��ۺ�MN��չ����
�ڶ�������һ���۵���ʹ��A����MN�ĵ�A�䴦����ʹ�ۺ۾�����B���õ��ۺ�BE��ͬʱ���õ��߶�BA�䣬EA�䣬չ������ͼ1��
������������EA�����ڵ�ֱ���۵�����B����AD�ĵ�B�䴦���õ��ۺ�EF��ͬʱ�õ��߶�B��F��չ������ͼ2��
��1��֤������ABE=30�㣻
��2��֤�����ı���BFB��EΪ���Σ�
���𰸡�������
��������
��1�����ݵ�M��AB���е��жϳ�A����EF���е㣬Ȼ���жϳ�BA����ֱƽ��EF�������߶δ�ֱƽ�����ϵĵ㵽���˵�ľ�����ȿɵ�BE=BF���ٸ��ݵ������������ߺ�һ�����ʿɵá�A��BE=��A��BF�����ݷ��۵����ʿɵá�ABE=��A��BE��Ȼ����ݾ��ε��ĸ��Ƕ���ֱ�Ǽ��㼴�ɵ�֤��
��2�����ݷ��۱任�����ʿɵ�BE=B��E��BF=B��F��Ȼ�����BE=B��E=B��F=BF���ٸ��������߶���ȵ��ı���������֤����
(1)�߶���AD��BC�غϣ��ۺ���MN��
���M��AB���е㣬
��A����EF���е㣬
�ߡ�BA��E=��A=90����
��BA����ֱƽ��EF��
��BE=BF��
���A��BE=��A��BF��
�ɷ��۵�����,��ABE=��A��BE��
���ABE=��A��BE=��A��BF��
���ABE=![]() ��90��=30����
��90��=30����
(2)����EA�����ڵ�ֱ���۵�,��B����AD�ϵĵ�B������
��BE=B��E,BF=B��F��
��BE=BF��
��BE=B��E=B��F=BF��
���ı���BFB��EΪ���Ρ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
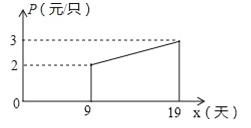
����Ŀ����ˮ��ij��ҵ�ӵ�һ��������������Ҫ����19������ɣ�Լ���������ӵij�����Ϊÿֻ4Ԫ��Ϊ��ʱ���������ҵ�������¹��ˣ����¹�������x����������������Ϊyֻ��y��x�������¹�ϵ��![]() ��
��
��1�����ڼ�����������������Ϊ260ֻ��
��2����ͼ�����x��������ÿֻ���ӵijɱ���pԪ��p��x֮��Ĺ�ϵ����ͼ�еĺ���ͼ�����̻���������x�촴�������ΪwԪ����w��x֮��ĺ�������ʽ��������ڼ�������������������Ƕ���Ԫ��������=�����۩��ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲������й��ɵĵ�����꣺![]()
![]()
![]() ���������˹��ɣ�
���������˹��ɣ�![]() ������Ϊ________��
������Ϊ________��![]() ������Ϊ_________.
������Ϊ_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����F������ABCD�Ķ���A��������A��D��B��1cm/s���ٶ������˶�����B��ͼ2�ǵ�F�˶�ʱ����FBC�����y��cm2����ʱ��x��s���仯�Ĺ�ϵͼ����a��ֵΪ��������

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC����AB=AC����E�DZ�AC��һ��������E��EF��BC��AB�ڵ�F
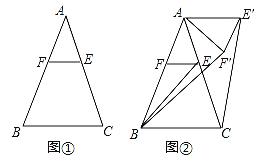
��1����ͼ�٣���֤��AE=AF��
��2����ͼ�ڣ�����AEF�Ƶ�A��ʱ����ת����0�㣼����144�㣩�õ���AE��F��������CE��BF�䣮
����BF��=6����CE���ij���
������EBC=��BAC=36�㣬��ͼ������ת����������CE���ABʱ��ֱ��д����ת�����Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ6����ʦ��234��ѧ������������������45����30��С����������1����2��С���������1000Ԫ��������2����һ��С���������1100Ԫ��
��1�����С��ÿ������Ѹ��Ƕ���Ԫ��
��2����ÿ����������Ҫ��һ����ʦ����������ò�����2300Ԫ������ʡǮ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
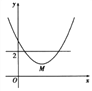
����Ŀ����֪������y=x2-4x+3��x���ཻ�ڵ�A,B(��A�ڵ�B���),����ΪM.ƽ�Ƹ�������,ʹ��Mƽ�ƺ�Ķ�Ӧ��M'����x����,��Bƽ�ƺ�Ķ�Ӧ��B'����y����.��ƽ�ƺ�������߽���ʽΪ����(����)
A. y=x2+2x+1 B. y=x2+2x-1 C. y=x2-2x+1 D. y=x2-2x-1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳�����1����λ���ȣ�Rt��ABC����������A(-2��2)��B(0��5)��C(0��2).
(1)����ABC�Ե�CΪ��ת������ת180�����õ���A1B1C���뻭����A1B1C��ͼ��.
(2)ƽ����ABC��ʹ��A�Ķ�Ӧ��A2����Ϊ(-2��-6)���뻭��ƽ�ƺ��Ӧ����A2B2C2��ͼ��.
(3)������A1B1C��ijһ����ת�ɵõ���A2B2C2����ֱ��д����ת���ĵ�����.

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com