
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(7,3),点E在边AB上,且AE=1,已知点P为y轴上一动点,连接EP,过点O作直线EP的垂线段,垂足为点H,在点P从点F(0, ![]() )运动到原点O的过程中,点H的运动路径长为 .
)运动到原点O的过程中,点H的运动路径长为 . 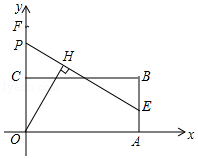
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
五个边长为![]() 的小正方形如图①放置,要求用两条线段将它们分割成三部分后把它们拼接成一个新的正方形.
的小正方形如图①放置,要求用两条线段将它们分割成三部分后把它们拼接成一个新的正方形.



小辰是这样思考的:图①中五个边长为![]() 的小正方形的面积的和为
的小正方形的面积的和为![]() ,拼接后的正方形的面积也应该是
,拼接后的正方形的面积也应该是![]() ,故而拼接后的正方形的边长为
,故而拼接后的正方形的边长为![]() ,因此想到了依据勾股定理,构造长为
,因此想到了依据勾股定理,构造长为![]() 的线段,即:
的线段,即:![]() ,因此想到了两直角边分别为
,因此想到了两直角边分别为![]() 和
和![]() 的直角三角形的斜边正好是
的直角三角形的斜边正好是![]() ,如图②,进而拼接成了一个便长为
,如图②,进而拼接成了一个便长为![]() 的正方形.
的正方形.
参考上面的材料和小辰的思考方法,解决问题:
(![]() )五个边长为
)五个边长为![]() 的小正方形如图④放置,类似图③,在图④中画出分割线和拼接后的正方形(只要画出一种即可).
的小正方形如图④放置,类似图③,在图④中画出分割线和拼接后的正方形(只要画出一种即可).
(![]() )十个边长为
)十个边长为![]() 的小正方形如图⑤放置,类似图③,在图⑤中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
的小正方形如图⑤放置,类似图③,在图⑤中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
(![]() )五个边长为
)五个边长为![]() 的小正方形如图⑥放置,类似图③,在图⑥中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
的小正方形如图⑥放置,类似图③,在图⑥中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长( ![]() ,要求结果精确得到0.1m)
,要求结果精确得到0.1m)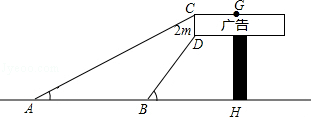
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当﹣1≤x≤3时,y<0;③3a+c=0;④若(x1 , y1)(x2、y2)在函数图象上,当0<x1<x2时,y1<y2 , 其中正确的是( ) 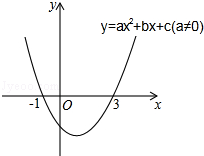
A.①②④
B.①③
C.①②③
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点D的对应点D′.
(1)根据特征画出平移后的△A′B′C′;
(2)利用网格的特征,画出AC边上的高BE并标出画法过程中的特征点;
(3)△A′B′C′的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.
(1)发现:在图1中, ![]() =;
=;
(2)应用:如图2,将△ADE绕点A旋转,请求出 ![]() 的值;
的值;
(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DE的中点,若BD⊥CE,请直接写出 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com