
����Ŀ���Ķ����⣺�á�ʮ����˷����ֽ���ʽ2x2��x��3�ķ�����
��i��������ϵ��2=1��2��
��ii�������3=��1��3=1������3�������㣺���������֮�͡���
1��3+2������1��=1 1������1��+2��3=5 1������3��+2��1=��1 1��1+2������3��=��5
��iii�����ֵڢ۸����������֮�͡��Ľ��1������3��+2��1=��1������һ����ϵ����1��
������x+1����2x��3��=2x2��3x+2x��3=2x2��x��3����2x2��x��3=��x+1����2x��3����
��������ͨ��ʮ�ֽ����߰������Ѷ�������ʽ�ֽ���ʽ�ķ���������ʮ����˷����������Ϸ������ֽ���ʽ��3x2+5x��12= ��
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��ƸְԱ�������Լס��ҡ�������������ѡ�˽����˱��Ժ����ԣ�����ɼ����־�Ϊ100�֣�Ȼ���ٰ�����ռ60%������ռ40%�����ѡ�˵��ۺϳɼ�������Ϊ100�֣���
���ǵĸ���ɼ����±���ʾ��
������ | ���Գɼ�/�� | ���Գɼ�/�� |
�� | 90 | 88 |
�� | 84 | 92 |
�� | x | 90 |
�� | 88 | 86 |
��1��ֱ��д����������ѡ�����Գɼ�����λ����
��2���ֵ�֪��ѡ�˱����ۺϳɼ�Ϊ87.6�֣������x��ֵ��
��3���������������ѡ�˵��ۺϳɼ��������ۺϳɼ�����ȷ����Ҫ��Ƹ��ǰ��������ѡ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������EΪBC���е㣬AB=4����BED=120�㣬��ͼ����Ӱ���ֵ����֮��Ϊ��������
A.![]()
B.2![]()
C.![]()
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����������ƽ��ֱ������ϵ�ڵ�λ����ͼ��ʾ����֪�� A ������Ϊ��3��0�����߶� AC�� BD �Ľ����� M��
��1��д���� M��B��C��D �����ꣻ
��2�����������еĵ� M �����ڵ�λ�þ���ƽ�ƺõ��� M����4��6��ʱ��д���� A��B��
C��D �Ķ�Ӧ�� A����B����C����D�������꣬������ı��� A��B��C��D�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABCD �У���E��O��F�ֱ��DZ�AB��AC��AD���е㣬����CE��CF��OE��OF��
��1����֤����BCE�ա�DCF��
��2����AB��BC����ʲô����ʱ���ı���AEOF�����Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���B=10�㣬��ACB=20�㣬AB=4cm����ABC��ʱ����תһ���ǶȺ�����ADE�غϣ��ҵ�Cǡ�ó�ΪAD���е㣮

��1��ָ����ת���ģ��������ת�Ķ�����
��2�������BAE�Ķ�����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������OABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ����AOC��45�㣬OC�� ![]() �����B������Ϊ��������.
�����B��������������.
A.�� ![]() ��1��
��1��
B.��1�� ![]() ��
��
C.�� ![]() ��1��
��1��
D.��1�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵ�У���A(o,m),��B(n,0)��m, n����![]() .
.
(1)��A,B������.
(2)��ͼ1, EΪ�ڶ�������ֱ��AB�ϵ�һ�㣬������![]() �����E�ĺ�����.
�����E�����.
(3)��ͼ2,ƽ���߶�BA��OC, B��O�Ƕ�Ӧ�㣬A��C�Ƕ�Ӧ�㣬����AC, EΪBA���ӳ�����һ�㣬����EO, OFƽ�֡�COE, AFƽ�֡�EAC, OF��AF�ڵ�F,����ABO+��OEB=��,����ͼ2�н�ͼ�β��������������F (�ú�����ʽ�ӱ�ʾ)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
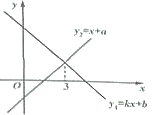
����Ŀ����֪һ�κ���![]() ��
��![]() ͼ����ͼ��ʾ�������н��ۣ���
ͼ����ͼ��ʾ�������н��ۣ���![]() ����
����![]() ���۹���
���۹���![]() �ķ���
�ķ���![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ���ܵ�
���ܵ�![]() ��
��![]() .������ȷ����_______(�����)��
.������ȷ����_______(�����)��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com