练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．填空：
    （1）已知（x+y）2=9，x2+y2=7，则xy=1．
    （2）已知（x+y）2=4，（x-y）2=3，则x2+y2=3.5．

    分析 （1）根据2xy=（x+y）2-（x2+y2）代入计算可得；
    （2）根据（x+y）2+（x-y）2=2（x2+y2）代入计算可得．

    解答 解：（1）∵（x+y）2=9，x2+y2=7，
    ∴2xy=（x+y）2-（x2+y2）=9-7=2，
    ∴xy=1；
    （2）∵（x+y）2=4，（x-y）2=3，
    ∴（x+y）2+（x-y）2=2（x2+y2）=7，
    ∴x2+y2=3.5．
    故答案为：（1）1，（2）3.5．

    点评 本题主要考查完全平方公式，将完全平方公式进行合适的变形是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．已知△ABC中，M为BC的中点，直线m  绕点A旋转，过B，M，C 分别作BD⊥m于点D，ME⊥m于点E，CF⊥m于点F．当直线m经过点B时，如图1，可以得到$EM=\frac{1}{2}CF$．
    （1）当直线m不经过B点，旋转到如图 2，图 3 的位置时，线段BD，ME，CF之间有怎样的数量关系，请直接写出你的猜想．
    图2，猜想：$ME=\frac{1}{2}（BD+CF）$；
    图3，猜想：$ME=\frac{1}{2}（CF-BD）$．
    （2）选择第（1）问中任意一种猜想加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

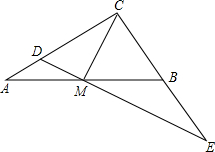    11．已知：如图，在△ABC中，∠ACB=90°，CM是斜边AB上的中线．
    （1）过点M作CM的垂线与AC和BD的延长线分别交于点D和点E，求证：△CDM∽△ABC；
    （2）过点M直线与AC和CB的延长线交于点D和点E，如果$\frac{DM}{MC}$=$\frac{AM}{ME}$，求证：CM⊥DE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，已知直线y=4-x与反比例函数y=$\frac{m}{x}$（m＞0，x＞0）的图象交于A，B两点，且点A的横坐标为1，与x轴，y轴分别相交于C，D两点．
    （1）求另一个交点B的坐标；
    （2）利用函数图象求关于x的不等式4-x＜$\frac{m}{x}$的解集；
    （3）求三角形AOB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．一个几何体的三视图如图所示，则这个几何体可能是（　　）
    A．圆锥B．球C．圆柱D．圆

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，点A，D是网格中的两点，现在将点A进行两次平移，第一次平移后的对应点为B第二次平移后的对应点为C，顺次连接ABCD四点，恰好是一个等腰梯形，请你在网格中画出图形，使这个等腰梯形的面积为12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，矩形ACBE中，AC=6，BC=8，D是AB上一动点，当AD=$\frac{11}{5}$时，∠BDC=2∠BAE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．由于现在人们生活水平的普遍提高，大家对自己的生存环境越来越关注，特别是对大气环境质量的关注，而空气中又以PM2.5对人体的危害性最大，某市环保局对该市市民进行了一项民意调查，以了解PM2.5浓度升高时对人们户外活动是否有影响，并制作了统计图表的一部分如下：
    公众对于户外活动的态度百分比
    A．没有影响a
    B．影响不大，还可以进行户外活动5%
    C．有影响，减少户外活动42%
    D．影响很大，尽可能不去户外活动b
    E．不关心这个问题6%
    （1）结合上述统计图表可得：a=2%，b=45%；
    （2）根据以上信息，请直接补全条形统计图；
    （3）若该市约400万人，根据上述信息，请你估计一下持有“影响很大，尽可能不去户外活动”这种态度的约有多少万人．（说明：“PM2.5”是指大气中危害健康的直径小于2.5微米的颗粒物，也称可入肺颗粒物）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，等腰Rt△ABC中，AB=AC，∠BAC=90°，BE平分∠ABC交AC于E，过C作CD⊥BE于D，DM⊥AB交BA的延长线于M，连接DA，
    （1）求$\frac{AB+BC}{BM}$的值；
    （2）求$\frac{BC-BA}{AM}$的值．

    查看答案和解析>>

    同步练习册答案