
 如图,AB是⊙O的直径,射线AM经过⊙O上的点E,弦AC平分∠MAB,过点C作CD⊥AM,垂足为D.
如图,AB是⊙O的直径,射线AM经过⊙O上的点E,弦AC平分∠MAB,过点C作CD⊥AM,垂足为D.分析 (1)根据题意画出图形,连接C,由等腰三角形的性质和角平分线的定义证出AM∥OC,即可得出结论;
(2)作OF⊥AM,垂足为F,则四边形OCDF是矩形,得出OF=CD,由勾股定理求出AF,由垂径定理即可求出AE的长.
解答 (1)作图如图1所示:
证明:连接OC,则OA=OC,
∴∠OAC=∠OCA
∵AC平分∠MAB,
∴∠OAC=∠MAC
∴∠OCA=∠MAC,
∴AM∥OC,
∵CD⊥AM,垂足为D,
∴∠CDM=90°
∴∠OCD=∠CDM=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:作OF⊥AM,垂足为F,
则AF=EF,四边形OCDF是矩形,
∴$OF=CD=2\sqrt{3}$,
在Rt△AOF中,∵AF2+OF2=OA2
∴$AF=\sqrt{O{A^2}-O{F^2}}=\sqrt{{{(\frac{1}{2}AB)}^2}-O{F^2}}=2$,
∴AE=2AF=4.
点评 本题考查了切线的判定、平行线的性质、等腰三角形的性质、矩形的判定与性质、勾股定理、垂径定理等知识;本题综合性强,有一定难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0 | B. | a<0 | C. | a<2 | D. | a>2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 填写下面证明过程中的推理依据:
填写下面证明过程中的推理依据:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周体育锻炼的时间 | |
| B. | 某中学调查全校753名学生的身高 | |
| C. | 某学校招聘教师,对应聘人员面试 | |
| D. | 鞋厂检查生产的鞋底能承受的弯折次数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
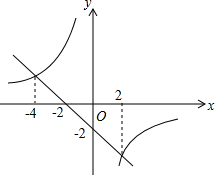 若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示,则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为( )
若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示,则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为( )| A. | 0<x≤2或x≤-4 | B. | -4≤x<0或x≥2 | C. | $-2\sqrt{2}$≤x<0或x$≥2\sqrt{2}$ | D. | x$≤-2\sqrt{2}$或0$<x≤2\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com