
【题目】知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC(填“>”“<”“=”);
(2)如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】宜昌四中男子篮球队在2016全区篮球比赛中蝉联冠军,让全校师生倍受鼓舞.在一次与第25中学的比赛中,运动员小涛在距篮下4米处跳起投篮,如图所示,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)运动员小涛的身高是1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,小涛跳离地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年2月初,在抵御新冠肺炎的工作中,全国各地口罩严重供应不足,某乡镇企业缝纫车间立即转岗做口罩以供应本地志愿者和卫生系统,该车间有技术工人15人,生产部为了合理制定口罩的日生产定额,统计了15人某天加工口罩数如下:
车间15名工人某一天加工口罩个数统计表
加工零件数/个 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)求这一天15名工人加工口罩数的平均数、中位数和众数.
(2)为了提高大多数工人的积极性,管理者准备试行“每天定额生产,超产有奖”的措施,假如你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 如图1,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF,四边形AEGF是矩形,写出矩形AEGF的面积y与BE的长x之间的函数关系式;
(2) 如图2,已知一长方形打印纸长20 cm,宽15 cm,现在要在打印纸上打印文稿,上下左右各留出一定距离.设留出的距离均为x cm,打印文稿面积为y cm2,试写出y与x之间的关系式,并求出x的取值范围.
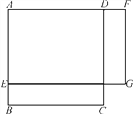
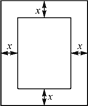
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区改善生态环境,实行生活垃圾的分类处理,将生活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为m,n,p,并且设置了相应的垃圾箱,“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共1 000吨生活垃圾,数据统计如下(单位:吨):
A | B | C | |
m | 400 | 100 | 100 |
n | 30 | 240 | 30 |
p | 20 | 20 | 60 |
请根据以上信息,试估计“厨房垃圾”投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
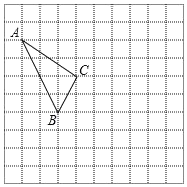
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,4),(﹣1,2).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)将△ABC向右平移2个单位长度,然后再向下平移3个单位长度,得到△A′B′C′,画出平移后的△A′B′C′.
(3)求S△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD,尺规作图:以点A为圆心,AB的长为半径画弧交AD于点F,分别以点B,F为圆心,以大于 BF的长为半径画弧交于点G,做射线AG交BC与点E,若BF=12,AB=10,则AE的长为( ).

A.17B.16C.15D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩与民主测评.A、B、C、D、E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评.结果如下表所示:
表1 演讲答辩得分表(单位:分)
A | B | C | D | E | |
甲 | 90 | 92 | 94 | 95 | 88 |
乙 | 89 | 86 | 87 | 94 | 91 |
表2 民主测评票数统计表(单位:张)
“好”票数 | “较好”票数 | “一般”票数 | |
甲 | 40 | 7 | 3 |
乙 | 42 | 4 | 4 |
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;
民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;
综合得分=演讲答辩得分×(1﹣a)+民主测评得分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)a在什么范围时,甲的综合得分高?a在什么范围时,乙的综合得分高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料(1),并利用(1)的结论解决问题(2)和问题(3).
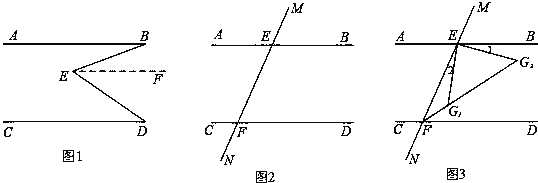
(1)如图1,AB∥CD,E为形内一点,连结BE、DE得到∠BED,求证:∠E=∠B+∠D
悦悦是这样做的:
过点E作EF∥AB.则有∠BEF=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
∴∠BEF+∠FED=∠B+∠D.
即∠BED=∠B+∠D.
(2)如图2,画出∠BEF和∠EFD的平分线,两线交于点G,猜想∠G的度数,并证明你的猜想.
(3)如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2,求证:∠FG1E+∠G2=180°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com