
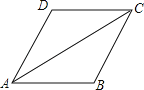
【题目】如图,AC是ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
(2)若AB=2,AC=2![]() ,求ABCD的面积.
,求ABCD的面积.
【答案】(1)详见解析;(2)2![]() .
.
【解析】
试题分析:(1)根据已知条件易证∠BAC=∠BCA,即可得出AB=BC;(2)连接BD交AC于O,易证四边形ABCD是菱形,根据菱形的性质可得AC⊥BD,OA=OC=![]() AC=
AC=![]() ,OB=OD=
,OB=OD=![]() BD,根据勾股定理求出OB的长,即可得BD的长,利用ABCD的面积=
BD,根据勾股定理求出OB的长,即可得BD的长,利用ABCD的面积=![]() ACBD,即可求得答案.
ACBD,即可求得答案.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA,
∵∠BAC=∠DAC,
∴∠BAC=∠BCA,
∴AB=BC;
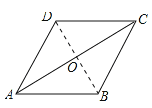
(2)解:连接BD交AC于O,如图所示:
∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,OA=OC=![]() AC=
AC=![]() ,OB=OD=
,OB=OD=![]() BD,
BD,
∴OB=![]() =
=![]() =1,
=1,
∴BD=2OB=2,
∴ABCD的面积=![]() ACBD=
ACBD=![]() ×2
×2![]() ×2=2
×2=2![]() .
.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】对三角形的高、中线和角平分线概念理解错误的是( )
A.直角三角形只有一条高
B.钝角三角形有两条高在三角形外部
C.锐角三角形的三条高、三条中线、三条角平分线分别交于一点
D.任意三角形都有三条高、三条中线、三条角平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖北襄阳第24题)
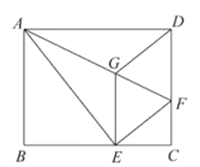
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)探究线段EG,GF,AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2![]() ,求的长.
,求的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
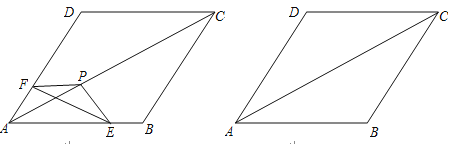
如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=![]() ,∠BAD=60°,且AB>
,∠BAD=60°,且AB>![]() .
.
⑴求∠EPF的大小;
⑵若AP=8,求AE+AF的值;
⑶若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,请直接写出AP长的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
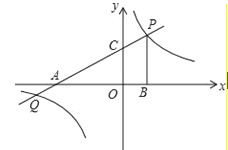
【题目】如图,直线y=![]() x+b,分别交x轴,y轴于点A、C,点P是直线AC与双曲线y=
x+b,分别交x轴,y轴于点A、C,点P是直线AC与双曲线y=![]() 在第一象限内的交点,过点P作PB⊥x轴于点B,若OB=2,PB=3.
在第一象限内的交点,过点P作PB⊥x轴于点B,若OB=2,PB=3.
(1)填空:k= ;
(2)求△ABC的面积;
(3)求在第一象限内,当x取何值时,一次函数的值小于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是 .
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com