
【题目】(1)如图1,△ABC中,作∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.
①求证:OE=BE.
②若△ABC的周长是25,BC=9,试求出△AEF的周长.
(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,若∠BAC=80°,∠PAC的度数?

【答案】(1)①见解析,②16;(2)50°
【解析】
(1)①由角平分线的性质、等腰三角形的性质和平行线的性质即可得到结论;②根据三角形的周长公式即可得到结论;
(2)延长BA,做PN⊥BD,PF⊥BA,PM⊥AC,根据角平分线的性质先证的PF=PM,得出∠FAP=∠PAC即可得出答案.
(1)①∵BO平分∠ABC
∴∠EBO=∠OBC
∵EF∥BC
∴∠EOB=∠OBC
∴∠EOB=∠EBO
∴OE=BE;
②同理可得:OF=FC
∵△ABC的周长是25,BC=9
∴△AEF的周长=AE+AF+EF=AE+AF+EB+FC=AB+AC=25-9=16;
(2)延长BA,做PN⊥BD,PF⊥BA,PM⊥AC,如图所示:
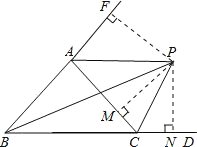
∵CP平分∠ACD,
∴PM=PN,
∵BP平分∠ABC,
∴PF=PN,
∴PF=PM,
∴∠FAP=∠PAC,
∴∠FAC=2∠PAC,
∵∠FAC+∠BAC=180°,
∴2∠PAC+∠BAC=180°
∴2∠PAC+80°=180°
∴∠PAC=50°.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是 度.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在⊙O的直径AB的延长线上,PC为⊙O的切线,点C为切点,连接AC,过点A作PC的垂线,点D为垂足,AD交⊙O于点E.
(1)如图1,求证:∠DAC=∠PAC;
(2)如图2,点F(与点C位于直径AB两侧)在⊙O上,![]() ,连接EF,过点F作AD的平行线交PC于点G,求证:FG=DE+DG;
,连接EF,过点F作AD的平行线交PC于点G,求证:FG=DE+DG;
(3)在(2)的条件下,如图3,若AE=![]() DG,PO=5,求EF的长.
DG,PO=5,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=3,BC=5,DE是BC的垂直平分线,DE分别交BC、AB于点D、E.
(1)求证:△ABC为直角三角形.
(2)求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图,先填空,然后回答问题

(1)由上而下第![]() 行的白球与黑球总数比第
行的白球与黑球总数比第![]() 行多 个.若第
行多 个.若第![]() 行白球与黑球的总数记作
行白球与黑球的总数记作![]() ,写出
,写出![]() 与
与![]() 的关系式.
的关系式.
(2)求出第![]() 行白球与黑球的总数可能是
行白球与黑球的总数可能是![]() 个吗?如果是,求出
个吗?如果是,求出![]() 的值;如果不是,说明理由.
的值;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x﹣1)2﹣4,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90°,∠A=34°,D,E 分别为 AB,AC 上一点,将△BCD,△ADE 沿 CD,DE 翻折,点 A,B 恰好重合于点 P 处,则∠ACP=_______________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com