
【题目】如图,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作
作![]() ,且
,且![]() ,点
,点![]() 在射线
在射线![]() 上(点
上(点![]() 不与点
不与点![]() 重合),且满足
重合),且满足![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .设
.设![]()
![]() .
.
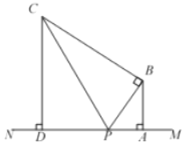
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)①线段![]() 的长是________;
的长是________;
②线段![]() 的长是_________;(用含
的长是_________;(用含![]() 的代数式表示)
的代数式表示)
(3)当![]() 为何值时,
为何值时,![]() 有最小值?并求出这个最小值.
有最小值?并求出这个最小值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)
;(3)![]() 时,
时,![]() 的最小值
的最小值![]() .
.
【解析】
(1)首先证明![]() ,然后根据相似三角形性质进一步得出
,然后根据相似三角形性质进一步得出![]() ,再结合勾股定理所得的
,再结合勾股定理所得的![]() 进一步对式子进行分析求解即可;
进一步对式子进行分析求解即可;
(2)①延长![]() 和
和![]() 交于点
交于点![]() ,通过证明
,通过证明![]() ,由此进一步得出
,由此进一步得出![]() ,然后再证明出
,然后再证明出![]() ,最后利用相似三角形性质求出CD即可;②先证明
,最后利用相似三角形性质求出CD即可;②先证明![]() ,据此进一步得出
,据此进一步得出![]() ,由此得出
,由此得出![]() ,最后进一步证明
,最后进一步证明![]() ,从而得出答案即可;
,从而得出答案即可;
(3)过点![]() 作
作![]() 于点
于点![]() ,通过证明
,通过证明![]() ,由此得出
,由此得出![]() ,然后得出
,然后得出![]() ,根据当点
,根据当点![]() 运动时,总有
运动时,总有![]() ,所以当点
,所以当点![]() 与点
与点![]() 重合,即
重合,即![]() 时,
时,![]() 的最小值
的最小值![]() ,由此求出
,由此求出![]() 的最小值,最后根据题意进一步求出
的最小值,最后根据题意进一步求出![]() 即可.
即可.
(1)在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() 90°,
90°,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
又根据勾股定理可得:![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)
①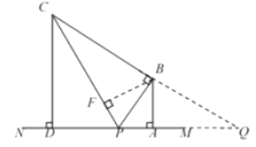
如图,延长![]() 和
和![]() 交于点
交于点![]() ,
,
∵![]() ,
,![]() ,且
,且![]() ,
,
∴![]() ,则有
,则有![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
②∵![]() ,
,![]() ,
,
∴∠ABP+∠APB=∠ABP+∠ABQ=90°,
∴∠APB=∠ABQ,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
由①知![]() ,结合
,结合![]() 可得:
可得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:①8;②![]() ;
;
(3)
如图,过点![]() 作
作![]() 于点
于点![]() ,
,
∵∠BAP=∠BFP,∠APB=∠FPB,PB=PB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴当点![]() 运动时,总有
运动时,总有![]() ,
,
∴当点![]() 与点
与点![]() 重合,即
重合,即![]() 时,
时,![]() 的最小值
的最小值![]() ,
,
则![]() 的最小值
的最小值![]() .
.
此时,如图所示,
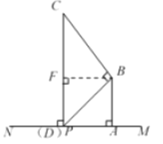
其中![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() (不符合题意,舍去).
(不符合题意,舍去).


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,将含30°角的
为坐标原点,将含30°角的![]() 放在第一象限,其中30°角的对边
放在第一象限,其中30°角的对边![]() 长为1,斜边
长为1,斜边![]() 的端点
的端点![]() ,
,![]() 分别在
分别在![]() 轴的正半轴,
轴的正半轴,![]() 轴的正半轴上滑动,连接
轴的正半轴上滑动,连接![]() ,则线段
,则线段![]() 的长的最大值是( )
的长的最大值是( )
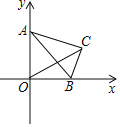
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
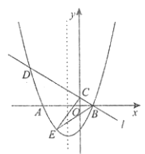
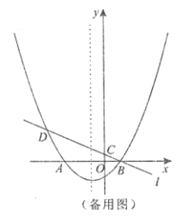
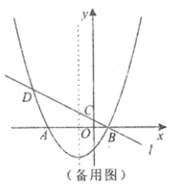
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),经过点
的左侧),经过点![]() 的直线
的直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() .
.
(1)则点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,抛物线的对称轴为__________;
的坐标为__________,抛物线的对称轴为__________;
(2)点![]() 是直线
是直线![]() 下方抛物线上的一点,当
下方抛物线上的一点,当![]() 时.求
时.求![]() 面积的最大值;
面积的最大值;
(3)设![]() 为抛物线对称轴上一点,点
为抛物线对称轴上一点,点![]() 在抛物线上,若以点
在抛物线上,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为矩形,求
为顶点的四边形为矩形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师在数学课上带领同学们做数学游戏,规则如下:
游戏规则
甲任报一个有理数数传给乙;
乙把这个数减![]() 后报给丙;
后报给丙;
丙再把所得的数的绝对值报给丁;
丁再把这个数的一半减![]() ,报出答案.
,报出答案.
根据游戏规则,回答下面的问题:
(1)若甲报的数为![]() ,则乙报的数为_________,丁报出的答案是_________;
,则乙报的数为_________,丁报出的答案是_________;
(2)若甲报的数为![]() ,请列出算式并计算丁报出的答案;
,请列出算式并计算丁报出的答案;
(3)若丁报出的答案是![]() ,则直接写出甲报的数.
,则直接写出甲报的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初期,天气炎热,水杯需求量大.双福育才中学门口某超市购进一批水杯,其中A种水杯进价为每个15元,售价为每个25元;B种水杯进价为每个12元,售价为每个20元
(1)该超市平均每天可售出60个A种水杯,后来经过市场调查发现,A种水杯单价每降低1元,则平均每天的销量可增加10个.为了尽量让学生得到更多的优惠,某天该超市将A种水杯售价调整为每个m元,结果当天销售A种水杯获利630元,求m的值.
(2)该超市准备花费不超过1600元的资金,购进A、B两种水杯共120个,其中B种水杯的数量不多于A种水杯数量的两倍.请为该超市设计获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形 ABCD 中,M,N,P,Q 分别为边 AB,BC,CD,DA 上的点(不与端点重合).对于任意矩形 ABCD,下面四个结论中:①存在无数个四边形 MNPQ 是平行四边形;②存在无数个四边形 MNPQ 是矩形;③存在无数个四边形 MNPQ 是菱形;④不存在四边形 MNPQ 是正方形.所有正确结论的序号是_________________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,建立直角坐标系.
轴,建立直角坐标系.

(Ⅰ)将矩形![]() 绕点
绕点![]() 逆时针旋转至矩形
逆时针旋转至矩形![]() ,如图1,
,如图1,![]() 经过点
经过点![]() ,求旋转角的大小和点
,求旋转角的大小和点![]() ,
,![]() 的坐标;
的坐标;
(Ⅱ)将图1中矩形![]() 沿直线
沿直线![]() 向左平移,如图2,平移速度是每秒1个单位长度.
向左平移,如图2,平移速度是每秒1个单位长度.
①经过几秒,直线![]() 经过点
经过点![]() ;
;
②设两矩形重叠部分的面积为![]() ,运动时间为
,运动时间为![]() ,写出重叠部分面积
,写出重叠部分面积![]() 与时间
与时间![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
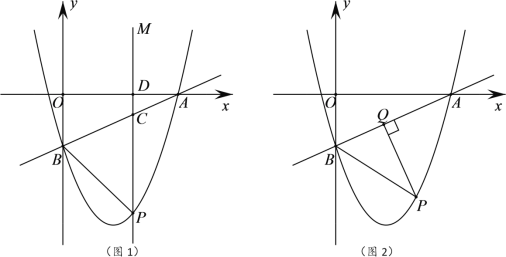
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像分别交x、y轴于点A、B,抛物线
的图像分别交x、y轴于点A、B,抛物线![]() 经过点A、B,点P为第四象限内抛物线上的一个动点.
经过点A、B,点P为第四象限内抛物线上的一个动点.
(1)求此抛物线对应的函数表达式;
(2)如图1所示,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;
(3)如图2所示,过点P作PQ⊥AB于点Q,连接PB,当△PBQ中有某个角的度数等于∠OAB度数的2倍时,请直接写出点P的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com