
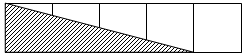
 如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )
如图,五个大小相同的小长方形拼在一起组成一个大长方形,那么图中阴影部分的面积是大长方形面积的( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:单选题
下列四张正方形硬纸片,分别将阴影部分剪去后,再沿虚线折叠,其中可以围成一个封闭长方体包装盒的是( )
A.  B.
B. 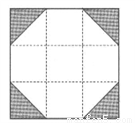 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
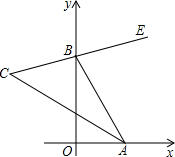 如图,在平面直角坐标系中,点A与点B分别在x轴与y轴的正半轴上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠C的大小是否随点A、B的移动而发生变化?如果保持不变,求出∠C的大小;如果随点A、B的移动而发生变化,请求出变化范围.
如图,在平面直角坐标系中,点A与点B分别在x轴与y轴的正半轴上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠C的大小是否随点A、B的移动而发生变化?如果保持不变,求出∠C的大小;如果随点A、B的移动而发生变化,请求出变化范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别切于L、M、N、P,且AB=10cm,CD=5cm,则四边形ABCD周长为30cm.
如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别切于L、M、N、P,且AB=10cm,CD=5cm,则四边形ABCD周长为30cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com