
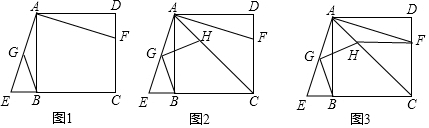
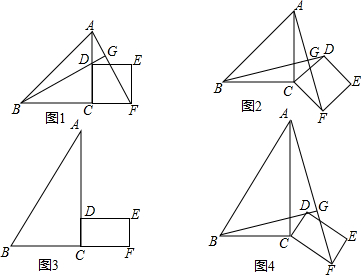
分析 (1)如图1中,由△ABE≌△ADF,推出∠AFD=∠E,由AG=GE,推出GB=GE=GA,推出∠E=∠GBE=∠AFD,由∠GBE+∠GBC=180°,推出∠AFD+∠GBC=180°即可;
(2)如图2中,连接BD交AC于O,连接OG、BH、取BH的中点K,连接GK、OK.只要证明O、H、G、B四点共圆,由AG=GE,AO=OC.推出OG∥CE,推出∠GOB=∠OBC=45°,即可解决问题;
(3)如图3中,如图3中,设OG交AB于T,GH交AB于P.,作HM⊥DF于M.只要证明∠EAB=∠GBP=∠PGT=∠HBO,推出tan∠EAB=tan∠HBO=$\frac{HO}{OB}$,由CH=3AH,OA=OC=OB,推出tan∠EAB=tan∠HBO=$\frac{HO}{OB}$=$\frac{1}{2}$,BE=DF=$\sqrt{10}$,在RtHMF中,利用勾股定理即可解决问题;
解答 (1)证明:如图1中,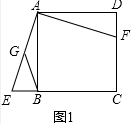
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠AEF=90°,
∴∠EAB=∠DAF,
∵∠ABE=∠ADF=90°,
∴△ABE≌△ADF,
∴∠AFD=∠E,
∵AG=GE,
∴GB=GE=GA,
∴∠E=∠GBE=∠AFD,
∵∠GBE+∠GBC=180°,
∴∠AFD+∠GBC=180°.
(2)证明:如图2中,连接BD交AC于O,连接OG、BH、取BH的中点K,连接GK、OK.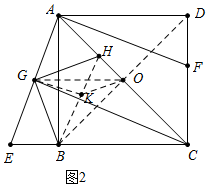
∵∠BGH=∠BOH=90°,BK=KH,
∴GK=KH=OK=KB,
∴O、H、G、B四点共圆,
∵AG=GE,AO=OC.
∴OG∥CE,
∴∠GOB=∠OBC=45°,
∴∠GOH=∠GBH=45°,∵∠BGH=90°,
∴∠GBH=∠GHB=45°,
∴GH=GB.
(3)解:如图3中,如图3中,设OG交AB于T,GH交AB于P.,作HM⊥DF于M.
∵OG∥EC,
AB⊥CE,
∴OG⊥AB,
易证∠EAB=∠GBP=∠PGT=∠HBO,
∴tan∠EAB=tan∠HBO=$\frac{HO}{OB}$,
∵CH=3AH,OA=OC=OB,
∴tan∠EAB=tan∠HBO=$\frac{HO}{OB}$=$\frac{1}{2}$,
∵AB=AD=2$\sqrt{10}$,
∴BE=DF=$\sqrt{10}$,
在Rt△HMF中,易证FM=$\frac{\sqrt{10}}{2}$,HM=$\frac{3}{2}$$\sqrt{10}$,
∴HF=$\sqrt{H{M}^{2}+F{M}^{2}}$=5.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、四点共圆、三角形的中位线定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考压轴题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.
如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.| A. | 7 | B. | 11 | C. | 13 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个游戏中奖的概率是$\frac{1}{10}$,则做10次这样的游戏一定会中奖 | |
| B. | 为了了解一批炮弹的杀伤半径,应采用全面调查的方式 | |
| C. | 一组数据8,7,7,10,6,7,9的众数和中位数都是7 | |
| D. | 若甲组数据的方差是0.1,乙组数据的方差是0.2,则乙组数据比甲组数据波动小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2•a5=a10 | B. | (π-3.14)0=0 | C. | ($\frac{1}{2}$)-2=$\frac{1}{4}$ | D. | $\sqrt{45}$-2$\sqrt{5}$=$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com