
 如图,△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角的平分线,CE⊥AE于点E.
如图,△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角的平分线,CE⊥AE于点E.分析 由角平分线定义得:∠BAD=∠CAD=$\frac{1}{2}$∠BAC和∠CAE=∠FAE=$\frac{1}{2}$∠FAC,则∠DAE=90°,再证明∠AEC=∠ECB=90°,由三个角是直角的四边形是矩形得出结论.
解答 证明:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC,
∵AE是∠BAC的外角的平分线,
∴∠CAE=∠FAE=$\frac{1}{2}$∠FAC,
∵∠BAC+∠FAC=180°,
∴∠DAC+∠EAC=$\frac{1}{2}$×180°=90°,
即∠DAE=90°,
∵CE⊥AE,
∴∠AEC=90°,
∵AB=AC,
∴∠B=∠ACB,
∵∠B+∠ACB+∠BAC=180°,
∴∠B+∠ACB=∠FAE+∠CAE,
∴∠FAE=∠B,
∴AE∥BC,
∴∠AEC+∠ECB=180°,
∴∠ECB=90°,
∴∠DAE=∠AEC=∠ECB=90°,
∴四边形ADCE是矩形.
点评 本题考查了角平分线的定义、等腰三角形的性质及矩形的判定,角平分线可以将一个角分成两个相等的角,同时要熟知等边对等角,掌握矩形的判定:①矩形的定义:有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形;本题利用了第②种判定方法判定四边形ADCE是矩形.


科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD中,点F在边AD上,BF的延长线交CD的延长线于E点,下列式子中能推出AD∥BC的式子是( )
如图,四边形ABCD中,点F在边AD上,BF的延长线交CD的延长线于E点,下列式子中能推出AD∥BC的式子是( )| A. | FD•EC=ED•BC | B. | AF•EF=BF•DF | C. | EF•EC=ED•BE | D. | AB•FD=DE•AF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
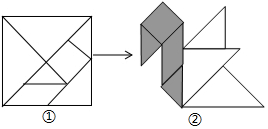 用边长为1的正方形纸板,制成一副七巧板(如图①),将它拼成“小天鹅”图案(如图②),其中阴影部分的面积为 ( )
用边长为1的正方形纸板,制成一副七巧板(如图①),将它拼成“小天鹅”图案(如图②),其中阴影部分的面积为 ( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{16}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
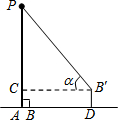 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB'的位置,测得∠PB'C=α=40°(B'C为水平线),测角仪B'D的高度为1米,则旗杆PA的高度表示为( )
小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB'的位置,测得∠PB'C=α=40°(B'C为水平线),测角仪B'D的高度为1米,则旗杆PA的高度表示为( )| A. | $\frac{1}{1+cos40°}$ | B. | $\frac{1}{1-cos40°}$ | C. | $\frac{1}{1+sin40°}$ | D. | $\frac{1}{1-sin40°}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com