
| a-2 |
| 2-a |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:阅读理解
| y |
| 2 |
| y |
| 2 |
| y |
| 2 |
| y |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年福建省龙岩市长汀县新桥二中九年级(上)第一次月考数学试卷(解析版) 题型:解答题
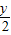 .
.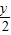 代入已知方程,得(
代入已知方程,得(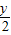 )2+
)2+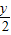 -1=0
-1=0查看答案和解析>>
科目:初中数学 来源:2013年广东省湛江市中考数学模拟试卷(七)(解析版) 题型:解答题
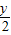 .
. 代入已知方程,得(
代入已知方程,得( )2+
)2+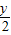 -1=0
-1=0查看答案和解析>>
科目:初中数学 来源:2012年贵州省黔西南州中考数学试卷(解析版) 题型:解答题
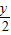 .
.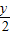 代入已知方程,得(
代入已知方程,得(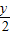 )2+
)2+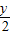 -1=0
-1=0查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com