
【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是 时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是 时,它们一定不全等.
【答案】钝角三角形或直角三角形,钝角三角形.
【解析】
试题分析:已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1.
证明:过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,则∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,在△BDC和△B1D1C1中,∵∠C=∠C1,∠BDC=∠B1D1C1,BC=B1C1,∴△BDC≌△B1D1C1,∴BD=B1D1,在Rt△BDA和Rt△B1D1A1中,∵AB=A1B1,BD=B1D1,∴Rt△BDA≌Rt△B1D1A1(HL),∴∠A=∠A1,在△ABC和△A1B1C1中,∵∠C=∠C1,∠A=∠A1,AB=A1B1,∴△ABC≌△A1B1C1(AAS).
同理可得:当这两个三角形都是钝角三角形或直角三角形时,它们也会全等,如图:△ACD与△ACB中,CD=CB,AC=AC,∠A=∠A,但:△ACD与△ACB不全等.
,故当这两个三角形其中一个三角形是锐角三角形,另一个是钝角三角形时,它们一定不全等.
故答案为:钝角三角形或直角三角形,钝角三角形.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
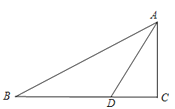
【题目】如图,已知在Rt△ABC中,∠C=900,AD是∠BAC的角分线.
(1)以AB上的一点O为圆心,AD为弦在图中作出⊙O.(不写作法,保留作图痕迹);
(2)试判断直线BC与⊙O的位置关系,并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 过B(﹣2,6),C(2,2)两点.
过B(﹣2,6),C(2,2)两点.

(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线![]() 向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
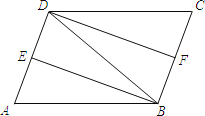
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com