
分析 利用非负数之和为零,则各自为零,进而求出a,b,c的值求出答案.
解答 解:∵2|a-1|+$\sqrt{2a-b}$+(c+b)2=0,
又∵|a-1|≥0,$\sqrt{2a-b}$≥0,(c+b)2≥0,
∴$\left\{\begin{array}{l}{a-1=0}\\{2a-b=0}\\{c+b=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=1}\\{b=2}\\{c=-2}\end{array}\right.$,
∴2a+b-c=2+2+2=6.
点评 此题主要考查了非负数的性质,正确得出a,b,c的值是解题关键.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:填空题
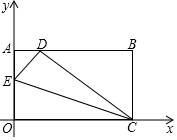 如图,有一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10,如图,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点处,则点E的坐标为(0,$\frac{10}{3}$).
如图,有一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10,如图,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点处,则点E的坐标为(0,$\frac{10}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
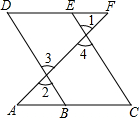 推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com