Question

如图，已知在Rt△ABC中，∠ACB=90°，AC=6，BC=8，BE平分∠ABC交AC于点E，EF⊥AB，垂足为F。
（1）求EF的长度；
（2）作CD⊥AB，垂足为D，CD与BE相交于G，试说明：CE=CG；
（3）连结FG，试说明：四边形CEFG是菱形。

Answer 1

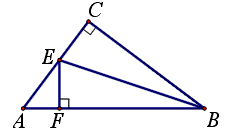
解：（1）∵BE平分∠ABC，∠ACB=90°，EF⊥AB，垂足为F， ∴EF=CE， 在△BFE与△BCE中，∠C=∠BFE=90°， ， ∴△BFE≌△BCE， ∴BF=BC=8， ∵在Rt△ABC中，∠ACB=90°，AC=6，BC=8， ∴AB=10， ∴AF=AB-BF=2， 设EF=x，则CE=x，AE=6-x， 在直角△AEF中，由勾股定理，得AE2=EF2+AF2， ∴（6-x）2=x2+22， 解得x=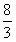； （2）∵在△BCE中，∠CEB=90°-∠CBE， ∠CGE=∠DGB=90°-∠DBG，∠CBE=∠DBG， ∴∠CEB=∠CGE， ∴CE=CG；
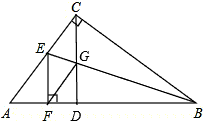
（3）∵CD⊥AB，EF⊥AB， ∴CD∥EF， ∵EF=CE，CE=CG， ∴EF=CG， ∴四边形CEFG是平行四边形， 又∵CE=CG， ∴平行四边形CEFG是菱形。