
【题目】如图,A、B两点在数轴上对应的数是a和b,且![]() ,点P为数轴上一动点,对应的数为x.
,点P为数轴上一动点,对应的数为x.
(1)求A、B两点间的距离;
(2)是否存在点P,使AP=![]() PB,若存在,求出x的值;若不存在,说明理由.
PB,若存在,求出x的值;若不存在,说明理由.
![]()
【答案】(1)8;(2)符合条件的x的值为0或15.
【解析】
(1)根据非负数的性质求得a、b的值,即可求得AB的长;(2)存在,分点P在A、B两点之间和点P在点B的右侧两种情况求x的值即可.
(1)∵![]() ,
,
∴a+5=0,b-3=0,
解得:a=-5,b=3,
∴点A表示的数为-5,点B表示的数为3,
∴AB=|a-b|=|-5-3|=8;
(2)存在,点P表示的数为x,
当点P在A、B两点之间时,AP=x+5,BP=3-x,
∵AP=![]() PB,
PB,
∴x+5=![]() (3-x),
(3-x),
解得x=0;
当点P在点B的右侧时,AP=x+5,BP=x-3,
∵AP=![]() PB,
PB,
∴x+5=![]() (x-3),
(x-3),
解得x=15.
综上,符合条件的x的值为0或15.


科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E. 
(1)求证:BD=BE;
(2)若DE=2,BD= ![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先填写表,通过观察后再回答问题:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ,y= ;
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;
≈ ;
②已知![]() =8.973,若
=8.973,若![]() =897.3,用含m的代数式表示b,则b= ;
=897.3,用含m的代数式表示b,则b= ;
(3)试比较![]() 与a的大小.
与a的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知数轴上点A、B分别表示a、b,且|b+6|与(a﹣9)2互为相反数,O为原点.
(1)a= ,b= ;
(2)若将数轴折叠点A与表示﹣10的点重合,则与点B重合的点所表示的数为 ;
(3)若点M、N分别从点A、B同时出发,点M以每秒1个单位长度的速度沿数轴向左匀速运动,点N以每秒2个单位长度的速度沿数轴向右匀速运动,N到点A后立刻原速返回,设运动时间为t(t>0)秒.①点M表示的数是 (用含t的代数式表示);②求t为何值时,2MO=MA;③求t为何值时,点M与N相距3个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸上的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形.在建立平面直角坐标系后,点B的坐标为(﹣2,﹣1).
(1)把△ABC向左平移4格后得到△A1B1C1,画出△A1B 1C1并写出点A1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得到△A2B2C,画出△A2B2C的图形并写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).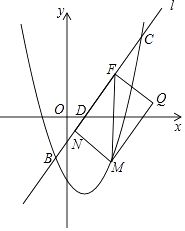
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线y=tx2(t≠0)也经过点A,过a与t之间的关系式;
(3)在(2)的条件下,已知a=﹣ ![]() ,直线l:y=
,直线l:y= ![]() x﹣1与抛物线y=tx2﹣
x﹣1与抛物线y=tx2﹣ ![]() x﹣7交于点B,C,与x轴,y轴交于点D,E,点M在抛物线y=tx2﹣
x﹣7交于点B,C,与x轴,y轴交于点D,E,点M在抛物线y=tx2﹣ ![]() x﹣7上,且点M的横坐标为m(0<m<6).MF∥y轴交于直线l于点F,点N在直线l上,且四边形MNFQ为矩形(如图),若矩形MNFQ的周长为P,求P的最大值.
x﹣7上,且点M的横坐标为m(0<m<6).MF∥y轴交于直线l于点F,点N在直线l上,且四边形MNFQ为矩形(如图),若矩形MNFQ的周长为P,求P的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com