
分析 (1)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解(1)$\left\{\begin{array}{l}{2x+5≥3(x+2)①}\\{\frac{x-1}{2}>\frac{x}{3}②}\end{array}\right.$,
由①得:x≤-1;
由②得:x>3,
∴原不等式组无解;
(2)$\left\{\begin{array}{l}{5x-1<3(x+1)①}\\{\frac{2x-1}{3}-\frac{5x+1}{2}≤1②}\end{array}\right.$
解①得 x<2;
解②得x≥-1;
∴原不等式组的解集为:-1≤x<2,
点评 此题考查了解一元一次不等式组,熟练掌握运算法则是解本题的关键.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
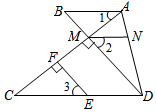 如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
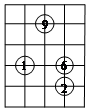 如图是一局围棋比赛的几手棋,为记录棋谱方便,模线用数字表示,纵线用字母表示,这样,黑棋
如图是一局围棋比赛的几手棋,为记录棋谱方便,模线用数字表示,纵线用字母表示,这样,黑棋 的位置可记为(B,20),白棋②的位置可记为(D,19),则白棋⑨的位置应记为( )
的位置可记为(B,20),白棋②的位置可记为(D,19),则白棋⑨的位置应记为( )| A. | (C,24) | B. | (24,C) | C. | (C,22) | D. | (22,C) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com