
【题目】扫地机器人能够自主移动并作出反应,是因为它发射红外信号反射回接收器,机器人在打扫房间时,若碰到障碍物则发起警报.若某一房间内A、B两点之间有障碍物,现将A、B两点放置于平面直角坐标系xOy中(如图),已知点A,B的坐标分别为(0,4),(6,4),机器人沿抛物线y=ax2﹣4ax﹣5a运动.若机器人在运动过程中只触发一次报警,则a的取值范围是_____.

【答案】﹣![]() <a<
<a<![]()
【解析】
根据题意可以知道抛物线与线段AB有一个交点,根据抛物线对称轴及其与y轴的交点即可求解.
解:由题意可知:
∵点A、B坐标分别为(0,4),(6,4),
∴线段AB的解析式为y=4.
机器人沿抛物线y=ax2﹣4ax﹣5a运动.
抛物线对称轴方程为:x=2,
机器人在运动过程中只触发一次报警,
所以抛物线与线段y=4只有一个交点.
所以抛物线经过点A下方.
∴﹣5a<4
解得a>﹣![]() .
.
4=ax2﹣4ax﹣5a,
△=0
即36a2+16a=0,
解得a1=0(不符合题意,舍去),a2=![]() .
.
当抛物线恰好经过点B时,
即当x=6,y=4时,
36a﹣24a﹣5a=4,
解得a=![]()
综上:a的取值范围是﹣![]() <a<
<a<![]()


科目:初中数学 来源: 题型:
【题目】随州市新水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;
(2)求最长的斜拉索AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
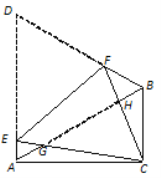
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°, △ABD是等边三角形,将四边形ACBD沿直线EF折叠,使D与C重合,CE与CF分别交AB于点G、H.
(1)求证:△AEG∽△CHG;
(2)△AEG与△BHF是否相似,并说明理由;
(3)若BC=1,求cos∠CHG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有![]() ,
,![]() 为原点,
为原点,![]() ,
,![]() ,将此三角形绕点
,将此三角形绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,抛物线
,抛物线![]()
![]() 过
过![]() 三点.
三点.
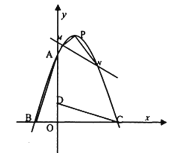
(1)求此抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)直线![]() 与抛物线交于
与抛物线交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值;
的值;
(3)抛物线的对称轴上是否存在一点![]() 使得
使得![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.
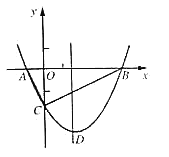
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
(3)点![]() 是抛物线对称轴上的一个动点,当
是抛物线对称轴上的一个动点,当![]() 周长最小时,求点
周长最小时,求点![]() 的坐标及
的坐标及![]() 的最小周长.
的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣bx+2b(b是常数).
(1)无论b取何值,该抛物线都经过定点 D.请写出点D的坐标.
(2)该抛物线的顶点是(m,n),当b取不同的值时,求n关于m的函数解析式.
(3)若在0≤x≤4的范围内,至少存在一个x的值,使y<0,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
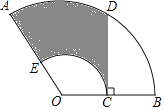
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )
A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“城市更美好、人民更幸福”,我市开展“三城联创”活动,环卫部门要求垃圾按![]() 三类分别装袋、投放,其中
三类分别装袋、投放,其中![]() 类指废电池,过期药品等有毒垃圾,
类指废电池,过期药品等有毒垃圾,![]() 类指剩余食品等厨余垃圾,
类指剩余食品等厨余垃圾,![]() 类指塑料、废纸等可回收垃圾,甲、乙两人各投放一袋垃圾.
类指塑料、废纸等可回收垃圾,甲、乙两人各投放一袋垃圾.
(1)甲投放的垃圾恰好是![]() 类的概率是 ;
类的概率是 ;
(2)用树状图或表格求甲、乙两人投放的垃圾是不同类别的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com