
在平面直角坐标系xOy,已知抛物线y=x2-2mx+m2-9.
(1)求证:无论m为何值,该抛物线与x轴总有两个交点;
(2)该抛物线与x轴交于A,B两点,点A在点B的左侧,且OA<OB,与y轴的交点坐标为(O,-5),求此抛物线的解析式;
(3)在(2)的条件下,抛物线的对称轴与x轴的交点为N,若点M是线段AN上的任意一点,过点M作直线MC⊥x轴,交抛物线于点C,记点C关于抛物线对称轴的对称点为D,点P是线段MC上一点,且满足MP=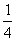 MC,连结CD,PD,作PE⊥PD交x轴与点E,问是否存在这样的点E,使得
MC,连结CD,PD,作PE⊥PD交x轴与点E,问是否存在这样的点E,使得 PE=PD,若存在,求出点E的坐标;若不存在,请说明理由.
PE=PD,若存在,求出点E的坐标;若不存在,请说明理由.
解:(l)△=(-2m)2 -4(m2 -9) =4m2-4m2+36 =36 >0,所以无论
m为何值,一元二次方程x2 -2mx+m2-9 =0总有两个不相
等的实数根;
 说明:指出抛物线开口向上,顶点在x轴下方,所以该 抛
说明:指出抛物线开口向上,顶点在x轴下方,所以该 抛
物线与x轴总有两交点 (亦可)
(2) ∵抛物线y=x2-2mx+m2-9与y轴交点生标为(0,-5),
∴-5=m2-9.解得m=t2.
∵抛物线y=x2-mx+m2-9与x轴交于A,B两点,点A在点B 的左侧,且0A<OB.
∴m=2.
∴抛物线的解析式为y =x2-4x-5.
(3)假设点E存在,
∵MC⊥EM,CD⊥MC,∴∠EMP= ∠PCD.
∵ PE⊥ PD.∴∠EPM=∠PDC.
∵PE= PD.∴△EPM≌△PDC.
∴PM=DC,EM=PD.
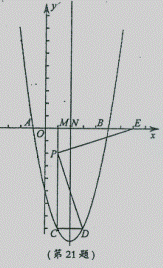
该抛物线y=x2-4x-5的对称轴x=2,N(2,O),A(一l,O),B(5,0)
设C(x0 ,y0),则D(4-x0,y0),P(x0, 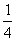 y0).(其中一l<x0<2,y0=x02-4x0-5)
y0).(其中一l<x0<2,y0=x02-4x0-5)
由CD= PM 得4 - 2xo=一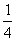 y0.
y0.
即4 - 2x0=一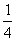 ( x02-4x0-5).
( x02-4x0-5).
解得x0=1或x0=1l(舍去)
∴M(1,O),C(1,一8) ∴P(1,一2). ∴PC =6.
∴ME= PC=6. ∴E(7,O)
∴点E存在其坐标为(7,O).


科目:初中数学 来源: 题型:
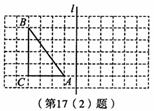
如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.
①sinB的值是 ;
②画出△ABC关于直线l对称的△A1B1C1(A与A1,B与B1,C与C1相对应).连接AA1,BB1,并计算梯形AA1B1B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
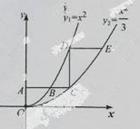
如图,平行于x轴的直线AC分别交函数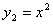 (x≥o)与
(x≥o)与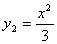 (x≥0)的图象于B、C两 点,过点c作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则
(x≥0)的图象于B、C两 点,过点c作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则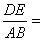
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)食品安全是关乎民生的问题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共1OO瓶,问A、B两种饮料各生产了多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
复习课中,教师给出关于x的函数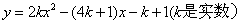 .
.
教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写道黑板上.
学生思考后,黑板上出现了一些结论,教师作为活动医院,又补充一些结论,并从中选择如下四条:
①存在函数,其图像经过(1,0)点;
②函数图像与坐标轴总有三个不同的交点;
③当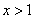 时,
时, 不是y随x的增大而增大就是y随x的增大而减小;
不是y随x的增大而增大就是y随x的增大而减小;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数。
教师:请你分别判断四条结论的真假,并给出理由.最后简单写出解决问题时所用的数学方法。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com