Question

已知一个直角三角形的面积为12cm²，周长为cm，那么这个直角三角形外接圆的半径是________cm．

Answer 1

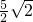
分析：如果设这个直角三角形的直角边是a，b，斜边是c，那么由题意得ab=12×2=24，a+b=12-c；根据勾股定理a²+b²=c²，可解得c=5．直角三角形外接圆其实就是以斜边的中点为圆心，斜边长的一半为半径的圆，因此它的半径是cm．
解答：如果设这个直角三角形的直角边是a，b，斜边是c，那么由题意得：
S_△=ab=12，a+b+c=12，
∴ab=24，a+b=12-c，
根据勾股定理得
a²+b²=c²，
（a+b）²-2ab=c²，
（12-c）²-48=c²，
解得c=5，
所以半径是cm．
点评：本题考查的是三角形的外接圆与外心以及勾股定理的运用，得出斜边的长是解决本题的关键．