
| 月销量y(个) | … | 160 | 200 | 240 | 300 | … |
| 每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
分析 (1)用原销量+因价格降低而增加的销量列出函数解析式即可得;
(2)根据月销量与固定成本的乘积为常数9600即可得;
(3)根据每个玩具的固定成本为30元,结合(2)中的函数解析式解方程可得;
(4)由月销量不超过400个得出x的范围,根据一次函数和反比例函数的性质求解可得.
解答 解:(1)y=300+2(280-x)=-2x+860;
(2)由表可知月销量与固定成本的乘积为常数,即Qy=9600,
∴Q=$\frac{9600}{y}$;
(3)当Q=30时,y=320=-2x+860,
解得:x=270,
则每个玩具的固定成本占销售单价的比例为$\frac{30}{270}$=$\frac{1}{9}$;
(4)由题意知-2x+860≤400,
解得:x≥230,
∵Q=$\frac{9600}{y}$=$\frac{9600}{-2x+860}$,
∴当x=230时,-2x+860取得最大值400,此时Q取得最小值24,
答:每个玩具的固定成本至少为24元,销售单价最低为230元.
点评 本题主要考查一次函数和反比例函数的应用,理解题意找到相等关系列出函数解析式,并熟练掌握一次函数和反比例函数的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
 小君同学在课外活动中观察吊车工作过程,绘制了如图所示的平面图形,已知吊车吊臂的支点O距离地面的高OO′=2米,当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.AB垂直地面O′B 于点B,A′B′垂直地面O′B 于点C,吊臂长度OA′=OA=10米且cosA=0.6,∠A′=30°.
小君同学在课外活动中观察吊车工作过程,绘制了如图所示的平面图形,已知吊车吊臂的支点O距离地面的高OO′=2米,当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.AB垂直地面O′B 于点B,A′B′垂直地面O′B 于点C,吊臂长度OA′=OA=10米且cosA=0.6,∠A′=30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
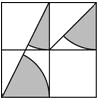 如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )| A. | $\frac{1}{4}$π | B. | $\frac{3}{4}$π | C. | $\frac{5}{8}$π | D. | $\frac{3}{8}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
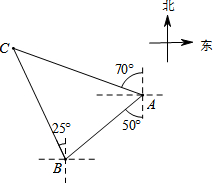 如图,国家规定休渔期间,我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只,可疑船只正沿北偏西25°方向航行,我国渔政船立即沿北偏西70°方向前去拦截,经过1.5小时刚好在C处拦截住可疑船只,求该可疑船只航行的平均速度.
如图,国家规定休渔期间,我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只,可疑船只正沿北偏西25°方向航行,我国渔政船立即沿北偏西70°方向前去拦截,经过1.5小时刚好在C处拦截住可疑船只,求该可疑船只航行的平均速度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
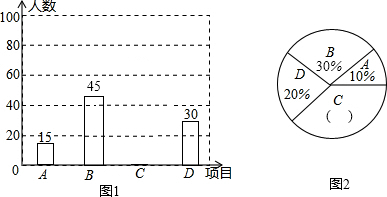
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com