
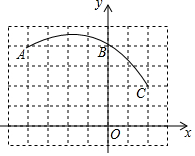
 如图,在单位长度为1的正方形网格中建立平面直角坐标系,一段圆弧经过网格的交点为A(-4,4),B(0,4),C(2,2).
如图,在单位长度为1的正方形网格中建立平面直角坐标系,一段圆弧经过网格的交点为A(-4,4),B(0,4),C(2,2).分析 (1)线段AB与线段BC的垂直平分线的交点即为点D.
(2)①利用两点间距离公式或勾股定理计算即可.②求出圆心角∠ADC的度数,利用弧长公式计算即可.③观察图形即可判断.
(3)求出直线AE的解析式即可解决问题.
解答 解:(1)如图,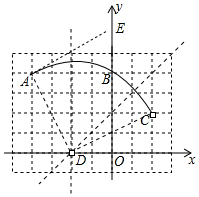 圆心D的位置如图所示.
圆心D的位置如图所示.
(2)①∵D(-2,0),B(0,4),
∴半径OB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
②∵直线AD的解析式为y=-2x-4,直线OC的解析式为y=$\frac{1}{2}$x+1,
∵-2×$\frac{1}{2}$=-1,
∴AD⊥DC,
∴∠ADC=90°,
∴$\widehat{AC}$的长=$\frac{90π•2\sqrt{5}}{180}$=2$\sqrt{5}$π.
③观察图象可知,此段圆弧所在的圆一共会经过3个整点,
度答案分别为2$\sqrt{5}$,2$\sqrt{5}$π,3.
(3)∵AE是切线,
∴AE⊥AD,
∴直线AE的解析式为y=$\frac{1}{2}$x+6,
∴点E坐标为(0,6).
点评 本题考查切线的判定和性质、一次函数的应用、弧长公式、勾股定理、两点间距离公式等整数,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 2x2 | B. | 2y2 | C. | y2-x2 | D. | x2-y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=70%×84 | B. | x=(1+70%)×84 | C. | 84=70%x | D. | 84=(1-70%)x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
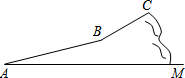 今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,.已知A点海拔191米,C点海拔791米.
今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,.已知A点海拔191米,C点海拔791米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com