
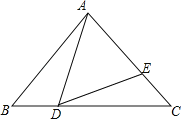
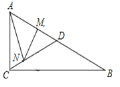
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=![]() ,点D、E分别在BC、AC上(点D不与点B、C重合),且∠ADE=45°,若△ADE是等腰三角形,则CE=_____.
,点D、E分别在BC、AC上(点D不与点B、C重合),且∠ADE=45°,若△ADE是等腰三角形,则CE=_____.
【答案】2﹣![]() 或
或![]() .
.
【解析】
当△ABD∽△DCE时,可能是DA=DE,也可能是ED=EA,所以要分两种情况求出CE长.
解:∵∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°.
∵∠ADE=45°,
∴∠B=∠C=∠ADE.
∵∠ADB=∠C+∠DAC,∠DEC=∠ADE+∠DAC,
∴∠ADB=∠DEC.
∵∠ADC+∠B+∠BAD=180,∠DEC+∠C+∠CDE=180°,
∴∠ADC+∠B+∠BAD=∠DEC+∠C+∠CDE,
∴∠EDC=∠BAD,
∴△ABD∽△DCE
∵∠DAE<∠BAC=90°,∠ADE=45°,
∴当△ADE是等腰三角形时,第一种可能是AD=DE.
∴△ABD≌△DCE.
∴CD=AB=![]() .
.
∴BD=2﹣![]() = CE,
= CE,
当△ADE是等腰三角形时,第二种可能是ED=EA.
∵∠ADE=45°,
∴此时有∠DEA=90°.
即△ADE为等腰直角三角形.
∴AE=DE=![]() AC=
AC=![]() .
.
∴CE=![]() AC=
AC=![]()
当AD=EA时,点D与点B重合,不合题意,所以舍去,
因此CE的长为2﹣![]() 或
或![]() .
.
故答案为:2﹣![]() 或
或![]() .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】某中学举行了“安全知识竞赛“,张岚将所有参赛选手的成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下:
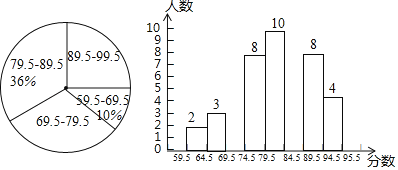
则下列结论不正确的是( )
A.本次比赛参赛选手共有50人
B.扇形统计图中“89.5~99.5“这一组人数占总参赛人数的百分比为24%
C.频数分布直方图中“84.5~89.5“这一组人数为8人
D.扇形统计图中“89.5~99.5“扇形的圆心角为90°
查看答案和解析>>
科目:初中数学 来源: 题型:
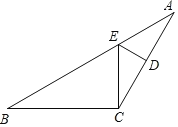
【题目】如图,在等腰△ABC中,AC=BC,∠ACB=4∠B,点D是AC边的中点,DE⊥AC,交AB于点E,连接CE.
(1)求∠BCE的度数;
(2)求证:AB=3CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
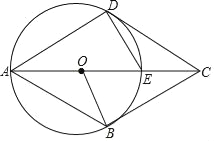
【题目】已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:BC是⊙O的切线;
(3)在(2)的条件下,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)当![]() ,
,![]() 时,求抛物线
时,求抛物线![]() 与
与![]() 轴的交点个数;
轴的交点个数;
(2)当![]() 时,判断抛物线
时,判断抛物线![]() 的顶点能否落在第四象限,并说明理由;
的顶点能否落在第四象限,并说明理由;
(3)当![]() 时,过点
时,过点![]() 的抛物线
的抛物线![]() 中,将其中两条抛物线的顶点分别记为
中,将其中两条抛物线的顶点分别记为![]() ,
,![]() ,若点
,若点![]() ,
,![]() 的横坐标分别是
的横坐标分别是![]() ,
,![]() ,且点
,且点![]() 在第三象限.以线段
在第三象限.以线段![]() 为直径作圆,设该圆的面积为
为直径作圆,设该圆的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,动点
,动点![]() 从点
从点![]() 出发沿
出发沿![]() 向终点
向终点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 向终点
向终点![]() 运动,两点速度均为每秒1个单位,两点同时出发,当其中一点到达终点后,运动停止,设运动时间为
运动,两点速度均为每秒1个单位,两点同时出发,当其中一点到达终点后,运动停止,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() (平方单位),则
(平方单位),则![]() 与
与![]() 之间的图象大致为( )
之间的图象大致为( )
A.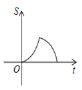 B.
B. C.
C.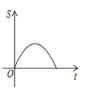 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
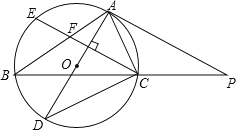
【题目】如图,AD是△ABC的外接圆⊙O的直径,点P在BC延长线上,PA是⊙O的切线,且∠B=35°.
(1)求∠PAC的度数.
(2)弦CE⊥AD交AB于点F,若AFAB=12,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
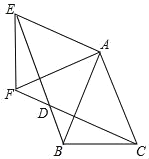
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com