
【题目】如图,一次函数y=ax﹣b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于B(0,﹣4),且OA=AB,△AOB的面积为6.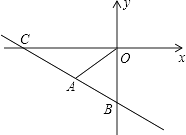
(1)求两个函数的解析式;
(2)若有一个点M(2,0),直线BM与AO交于点P,求点P的坐标;
(3)在x轴上是否存在点E,使S△ABE=5?若存在,求点E的坐标;若不存在,请说明理由.
【答案】
(1)
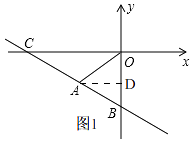
解:如图1,
作AD⊥OB轴于D,
∵B(0,﹣4),
∴OB=4,
∵OA=AB,
∴OD=BD= ![]() OB=2,
OB=2,
∵S△AOB=6,
∴S△AOB= ![]() OBAD=
OBAD= ![]() ×4AD=6,
×4AD=6,
∴AD=3
而点A在第三象限内,则A(﹣3,﹣2),
又点A在y=kx上,
∴﹣2=﹣3k,∴k= ![]() ,
,
∴正比例函数解析式为:y= ![]() x,
x,
又y=ax﹣b通过A、B,
∴ ![]() ,
,
∴ 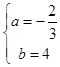
∴一次函数解析式为:y=﹣ ![]() x﹣4
x﹣4
(2)
解:由(1)知,正比例函数解析式为:y= ![]() x①,
x①,
∵B(0,﹣4),M(2,0),
∴直线BM的解析式为y=2x﹣4②,
联立①②得,点P(3,2)
(3)
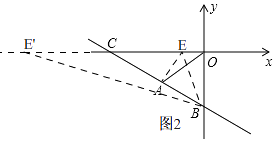
解:如图2,
由(1)知,一次函数解析式为:y=﹣ ![]() x﹣4
x﹣4
∴C(﹣6,0)
∵点E在x轴上,设E(x,0),
∴CE=|x+6|,
∵S△ABE=5,
S△ABE=S△BCE﹣S△ACE= ![]() BE|yB|﹣
BE|yB|﹣ ![]() BE|yA|=
BE|yA|= ![]() BE(|yB|﹣|yA|)=
BE(|yB|﹣|yA|)= ![]() |x+6|(4﹣2)=|x+6|=5
|x+6|(4﹣2)=|x+6|=5
∴x=﹣1或x=﹣11;
∴E(﹣1,0)或(﹣11,0)能够使得△ABE的面积为5.
【解析】(1)利用等腰三角形的三线合一得出OD= ![]() OB=2,再用三角形的面积求出AD=3,即可得出结论;(2)利用待定系数法求出直线BM的解析式和正比例函数解析式,联立即可得出结论;(3)利用三角形的面积的差,建立方程求解即可得出结论.
OB=2,再用三角形的面积求出AD=3,即可得出结论;(2)利用待定系数法求出直线BM的解析式和正比例函数解析式,联立即可得出结论;(3)利用三角形的面积的差,建立方程求解即可得出结论.
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在一块长为a,宽为2b的长方形铁皮中,以2b为直径分别剪掉两个半圆, 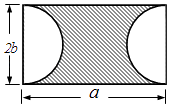
(1)求剩下铁皮的面积(用含a,b的式子表示);
(2)当a=4,b=1时,求剩下铁皮的面积是多少?(π取3.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
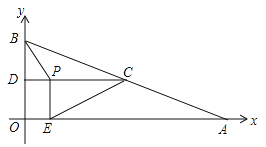
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,![]() ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为 .
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一个四边形OABC,其中CB∥x轴,OC=3,BC=2,∠OAB=45°. 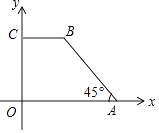
(1)求点A,B的坐标;
(2)求出直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条纸带,较长的一条长23 cm,较短的一条长15 cm.把两条纸带剪下同样长的一段后,剩下的两条纸带中,要求较长的纸带的长度不少于较短的纸带长度的两倍,那么剪下的长度至少是( )
A. 6cm B. 7cm C. 8cm D. 9cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com