
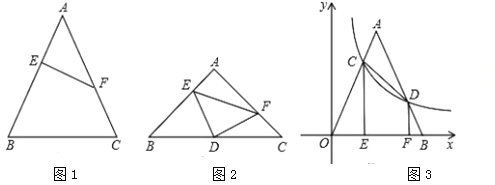
【题目】如图1,等腰![]() 中,点
中,点![]() 分别在腰
分别在腰![]() 上,连结
上,连结![]() ,若
,若![]() ,则称
,则称![]() 为该等腰三角形的逆等线.
为该等腰三角形的逆等线.
(1)如图1,![]() 是等腰
是等腰![]() 的逆等线,若
的逆等线,若![]() ,求逆等线
,求逆等线![]() 的长;
的长;
(2)如图2,若直角![]() 的直角顶点
的直角顶点![]() 恰好为等腰直角
恰好为等腰直角![]() 底边
底边![]() 上的中点,且点
上的中点,且点![]() 分别在
分别在![]() 上,求证:
上,求证:![]() 为等腰
为等腰![]() 的逆等线;
的逆等线;
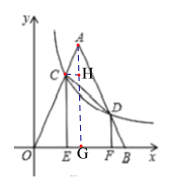
(3)如图3,等腰![]() 的顶点
的顶点![]() 与原点重合,底边
与原点重合,底边![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() ,若
,若![]() 恰为
恰为![]() 的逆等线,过点
的逆等线,过点![]() 分别作
分别作![]() 轴于点
轴于点![]() 轴于点
轴于点![]() ,已知
,已知![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)由![]() 是等腰
是等腰![]() 的逆等线,得CF=AE=2,根据勾股定理,即可得到答案;
的逆等线,得CF=AE=2,根据勾股定理,即可得到答案;
(2)连接AD,根据等腰直角三角形的性质,得AD=DC=BD,∠EAD=∠FCD=45°,AD⊥BC,从而得∠ADE=∠CDF,进而证:ADECDF(ASA),即可得到结论;
(3)设OF=x,则DF=![]() ,作AG⊥OB于点G,CH⊥AG于点H,易证△ACH△DBF(AAS),得EG=CH=BF,AH=DF,进而得EG=x4,由△ACH~△COE,得
,作AG⊥OB于点G,CH⊥AG于点H,易证△ACH△DBF(AAS),得EG=CH=BF,AH=DF,进而得EG=x4,由△ACH~△COE,得![]() ,列出关于x的方程,即可求解.
,列出关于x的方程,即可求解.
(1)∵![]() 是等腰
是等腰![]() 的逆等线,
的逆等线,
∴CF=AE=2,
∵![]() ,
,
∴AF=5-2=3,
∵![]() ,
,
∴![]() ;
;
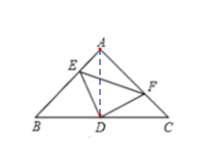
(2)连接AD,
∵点![]() 为等腰直角
为等腰直角![]() 底边
底边![]() 上的中点,
上的中点,
∴AD=DC=BD,∠EAD=∠FCD=45°,AD⊥BC,
∵∠EDF=90°,
∴∠ADE+∠ADF=∠CDF+∠ADF=90°,
∴∠ADE=∠CDF,
∴ADECDF(ASA),
∴AE=CF,
∴![]() 为等腰
为等腰![]() 的逆等线;
的逆等线;
(3)设OF=x,则DF=![]() ,
,
作AG⊥OB于点G,CH⊥AG于点H,
∵CD为![]() 的逆等线,
的逆等线,
∴AC=BD,
∵![]() 是等腰三角形,
是等腰三角形,
∴∠ACH=∠AOB=∠DBF,∠AHC=∠AGO=∠DFB=90°,
在△ACH和△DBF中
∵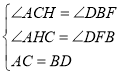 ,
,
∴△ACH△DBF(AAS),
∴EG=CH=BF,AH=DF,
又∵AO=AB,且AG⊥OB,
∴OG=BG,
∴GF=BGBF=OGEG=OE,
∴EG=x22=x4,
∵△ACH~△COE,
∴![]() ,即:
,即: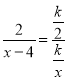 ,化简得:x24x4=0,解得:x1=
,化简得:x24x4=0,解得:x1=![]() ,x2=
,x2= ![]() (舍去),
(舍去),
∴OF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,地面BD上两根等长立柱AB,CD之间有一根绳子可看成抛物线y=0.1x2﹣0.8x+5.
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为5米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面2米,求MN的长;
(3)将立柱MN的长度提升为5米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为![]() .设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
.设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
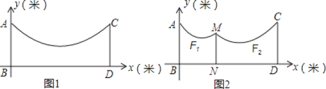
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数![]() 的图象,下列结论:
的图象,下列结论:
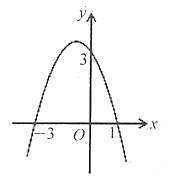
①二次三项式![]() 的最大值为
的最大值为![]() ;
;
![]() 使
使![]() 成立的
成立的![]() 的取值范围是
的取值范围是![]() ;
;
![]() 一元二次方程
一元二次方程![]() ,当
,当![]() 时,方程总有两个不相等的实数根;
时,方程总有两个不相等的实数根;
![]() 该抛物线的对称轴是直线
该抛物线的对称轴是直线![]() ;
;
![]()
其中正确的结论有______________ (把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
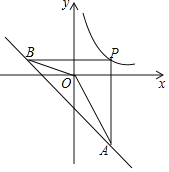
【题目】如图,P为反比例函数y=![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若∠AOB=135°,则k的值是( )
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若∠AOB=135°,则k的值是( )
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
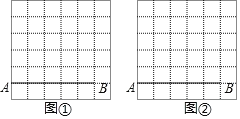
【题目】图①、图②都是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB的端点都在格点上,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹.
(1)在图①中画出一个以AB为一边的等腰△ABC,使点C在格点上,且面积为![]() ;
;
(2)在图②中画出一个以AB为一边的等腰△ABD,使点D在格点上,且tan∠DAB=3,并直接写出△ABD底边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=![]() OB.
OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
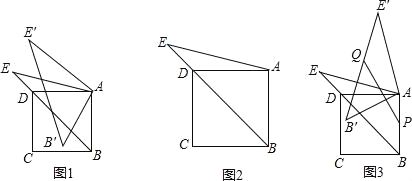
【题目】已知,正方形ABCD的边长为4,点E是对角线BD延长线上一点,AE=BD.将△ABE绕点A顺时针旋转α度(0°<α<360°)得到△AB′E′,点B、E的对应点分别为B′、E′.
(1)如图1,当α=30°时,求证:B′C=DE;
(2)连接B′E、DE′,当B′E=DE′时,请用图2求α的值;
(3)如图3,点P为AB的中点,点Q为线段B′E′上任意一点,试探究,在此旋转过程中,线段PQ长度的取值范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com