
【题目】如图,将矩形ABCD沿BD翻折,点C落在P点处,连接AP.若∠ABP=26°,则∠APB=___________

【答案】32°
【解析】分析:根据轴对称的性质和矩形的性质可以得出AB=DP,AP∥BD,进而得出∠APB的度数.
详解:∵△BDC与△BDE关于BD对称,
∴△BDC≌△BDP,
∴BP=BC,DP=DC,∠DBP=∠DBC.
∵四边形ABCD是矩形,
∴AB=CD=DP,AD=BC=BP,AD∥BC,
∴∠ADB=∠CBD,
∴∠PBD=∠ADB,
∴BF=DF,
∴BPBF=ADDF,
∴AF=PF,
∴∠FAP=∠FPA,
∵∠AFP=∠BFD,
∴2∠PAF=2∠ADB,
∴∠PAF=∠ADB,
∴AP∥BD,
∴∠APB=∠PBD,
∵∠ABP=26°,
∴∠CBD=∠DBP=![]() (90°26°)=32°,
(90°26°)=32°,
则∠APB=32°.
故答案为:32°.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知与填空:如图①,直线![]() ,求证:
,求证:![]() .
.
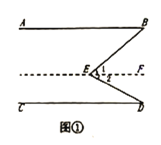
阅读下面的解答过程,并填上适当的理由,
解:过点![]() 作直线
作直线![]() ,
,
![]() ( )
( )
![]() (已知),
(已知),![]() ,
,
![]() ( )
( )
![]() ( )
( )
![]() ,
,
![]() ( )
( )
应用与拓展:如图②,直线![]() ,若
,若![]() .
.
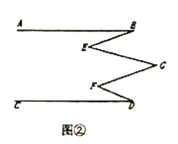
则![]() 度
度
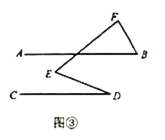
方法与实践:如图③,直线![]() ,若
,若![]() ,则
,则![]() 度.
度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口B和点落水点C在同一直线上,洗手盆及水龙头的相关数据如图2.(参考数据:sin37°=![]() ,cos37°=
,cos37°=![]() ,tan37°=
,tan37°=![]() )
)
求把手端点A到BD的距离;
求CH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() 给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1,
给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1,![]() ),(2,
),(2,![]() ),都是“同心有理数对”.
),都是“同心有理数对”.
(1)数对(﹣2,1),(3,![]() )是 “同心有理数对”的是__________.
)是 “同心有理数对”的是__________.
(2)若(a,3)是“同心有理数对”,求a的值;
(3)若(m,n)是“同心有理数对”,则(﹣n,﹣m) “同心有理数对”(填“是”或“不是”),说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,弧AB=弧AC,AP是⊙O的切线,交BO的延长线于点P
(1) 求证:AP∥BC
(2) 若tan∠P=![]() ,求tan∠PAC的值
,求tan∠PAC的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①两点之间,直线最短.
②三条直线两两相交,最少有三个交点.
③射线![]() 和射线
和射线![]() 是同一条射线.
是同一条射线.
④同角(或等角)的补角相等.
⑤在同一平面内,垂直于同一条直线的两条直线互相平行.
⑥绝对值等于它本身的数是非负数.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,已知∠AOC=75°,∠BOE :∠DOE=2:3.

(1)求∠BOE的度数;
(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明箱子中有2个红球,1个黑球和1个白球,四个小球的形状、大小完全相同.
(1)从中随机摸取1个球,则摸到黑球的概率为 ;
(2)小明和小贝做摸球游戏,游戏规则如下.

你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com