
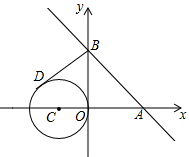
 如图,直线y=-x+2与x轴、y轴分别交于点A,B,C(-1,0),且圆C的半径为1.若BD切圆C于点D,点D在第二象限,求点D的坐标.
如图,直线y=-x+2与x轴、y轴分别交于点A,B,C(-1,0),且圆C的半径为1.若BD切圆C于点D,点D在第二象限,求点D的坐标. 分析 如图连接CB,OD交点为E.先求得点B的坐标,然后求得直线CB的解析式,然后根据OD⊥CB,从而可求得直线OD的解析式,然后求得CB与OD的交点E的坐标,然后利用中点坐标公式可求得点D的坐标.
解答 解:如图连接CB,OD交点为E.
将x=0代入y=-x+2得:y=2,
∴点B的坐标为(0,2).
设直线BC的解析式为y=kx+b.
根据题意得;$\left\{\begin{array}{l}{-k+b=0}\\{b=2}\end{array}\right.$
解得:b=2,k=2.
∴直线BC的解析式为y=2x+2.
∵OD⊥BC,
∴DO的解析式为y=-$\frac{1}{2}x$.
将y=-$\frac{1}{2}x$与y=2x+2联立得:$\left\{\begin{array}{l}{y=-\frac{1}{2}x}\\{y=2x+2}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=-\frac{4}{5}}\\{y=\frac{4}{10}}\end{array}\right.$.
∴点E的坐标为($-\frac{4}{5}$,$\frac{4}{10}$).
设点D的坐标为(x,y),则$\frac{x+0}{2}=-\frac{4}{5}$,$\frac{y+0}{2}=\frac{4}{10}$.
解得x=$-\frac{8}{5}$,y=$\frac{4}{5}$.
所以点D的坐标为($-\frac{8}{5}$,$\frac{4}{5}$).
点评 本题主要考查的是切线的性质、一次函数的综合应用,掌握中线段的中点坐标公式是解题的关键.


科目:初中数学 来源: 题型:解答题
 由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
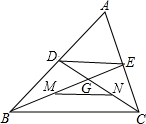 如图,在△ABC中,中线BE与中线CD交于点G,若M为BE的中点,N为CD的中点,则$\frac{MN}{DE}$=$\frac{1}{2}$.
如图,在△ABC中,中线BE与中线CD交于点G,若M为BE的中点,N为CD的中点,则$\frac{MN}{DE}$=$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com