
【题目】如图,已知直线![]() 经过点
经过点![]() 和
和![]() ,分别与x轴、y轴交于A、B两点.
,分别与x轴、y轴交于A、B两点.
(1)求直线![]() 的解析式:
的解析式:
(2)若把横、纵坐标均为整数的点称为格点,则图中阴影部分(不包括边界)所含格点的个数有 个;
(3)作出点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,则点
,则点![]() 的坐标为 ;
的坐标为 ;![]()
(4)若在直线![]() 和
和![]() 轴上分别存在一点
轴上分别存在一点![]() 使
使![]() 的周长最短,请在图中标出点
的周长最短,请在图中标出点![]() (不写作法,保留痕迹).
(不写作法,保留痕迹).

【答案】(1)![]() ;(2)10;(3)作图见解析,D(6,2);(4)作图见解析
;(2)10;(3)作图见解析,D(6,2);(4)作图见解析
【解析】
(1)先利用待定系数法求得直线AB的解析式为![]() ;
;
(2)分别把x=2、3、4、5代入,求出对应的纵坐标,从而得到图中阴影部分(不包括边界)所含格点的坐标;
(3)首先作出点C关于直线AB的对称点D,根据直线AB的解析式可知△OAB是等腰直角三角形,然后根据轴对称的性质即可求出点D的坐标;
(4)作出点C关于直线y轴的对称点E,连接DE交AB于点M,交y轴于点N,则此时△CMN的周长最短.
(1)设直线AB的解析式为![]() ,
,
把(1,5),(4,2)代入得,![]() ,
,
解得![]() ,
,
∴直线AB的解析式为![]() ;
;
(2)当x=2,y=4;
当x=3,y=3;
当x=4,y=2;
当x=5,y=1.
∴图中阴影部分(不包括边界)所含格点的有:
(1,1),(1,2),(1,3),(1,4),
(2,1),(2,2),(2,3),
(3,1),(3,2),
(4,1).
一共10个;
故答案为:10;
(3)如图,点D就是所求作的点;
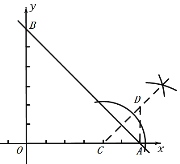
∵直线![]() 与
与![]() 轴、y轴交于A、B两点,
轴、y轴交于A、B两点,
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ;
;
∴A点坐标为(6,0),B点坐标为(0,6),
∴OA=OB=6,∠OAB=45°.
∵点C关于直线AB的对称点为D,点C(4,0),
∴AD=AC=2,AB⊥CD,
∴∠DAB=∠CAB=45°,
∴∠DAC=90°,
∴点D的坐标为(6,2);
(4)如图,点M、N就是所求的点;
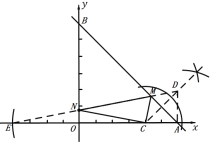
作出点C关于直线y轴的对称点E,连接DE交AB于点M,交y轴于点N,则NC=NE,点E(-4,0).
又∵点C关于直线AB的对称点为D,
∴CM=DM,
∴△CMN的周长=CM+MN+NC=DM+MN+NE=DE,此时周长最短.


科目:初中数学 来源: 题型:
【题目】在数轴上有三个点![]() 、
、![]() 、
、![]() ,如图所示.
,如图所示.
![]()
(1)将点![]() 向左平移4个单位,此时该点表示的数是________;
向左平移4个单位,此时该点表示的数是________;
(2)将点![]() 向左平移3个单位得到数
向左平移3个单位得到数![]() ,再向右平移2个单位得到数
,再向右平移2个单位得到数![]() ,则
,则![]() ,
,![]() 分别是多少?
分别是多少?
(3)怎样移动![]() 、
、![]() 、
、![]() 中的两点,使三个点表示的数相同?你有几种方法?
中的两点,使三个点表示的数相同?你有几种方法?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个体户购进一批时令水果,20天销售完毕,他将本次销售情况进行了跟踪记录,根据所记录的数据绘制如下的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图(1)所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图(2)所示。(销售额=销售单价×销售量)
(1)直接写出y与x之间的函数解析式;
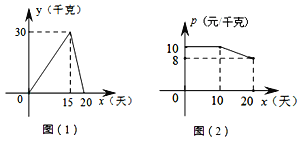
(2)分别求第10天和第15天的销售额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中,“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
(1)求此抛物线的解析式;
(2)设E是线段AB上的动点,作EF∥AC交BC于F,连接CE,当△CEF的面积是△BEF面积的2倍时,求E点的坐标;
(3)若P为抛物线上A、C两点间的一个动点,过P作y轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
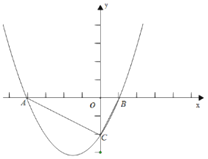
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
三角形的直角边长/ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
阴影部分的面积/ | 398 | 392 | 382 | 368 | 350 | 302 | 272 | 200 |

(1)在这个变化过程中,自变量、因变量各是什么?
(2)请将上述表格补充完整;
(3)当等腰直角三角形的直角边长由![]() 增加到
增加到![]() 时,阴影部分的面积是怎样变化的?
时,阴影部分的面积是怎样变化的?
(4)设等腰直角三角形的直角边长为![]() ,图中阴影部分的面积为
,图中阴影部分的面积为![]() ,写出
,写出![]() 与
与![]() 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,
两点,![]() 于点
于点![]() ,点
,点![]() 为直线
为直线![]() 上不与点
上不与点![]() 重合的一个动点.
重合的一个动点.
(1)求线段![]() 的长;
的长;
(2)当![]() 的面积是6时,求点
的面积是6时,求点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,若存在,请直接写出所有符合条件的点
全等,若存在,请直接写出所有符合条件的点![]() 的坐标,否则,说明理由.
的坐标,否则,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A![]() ,B(-1,2)是一次函数
,B(-1,2)是一次函数![]() 与反比例函数
与反比例函数![]()
(![]() )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,BC=2,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com