
【题目】背景知识:
如图(2),在Rt△ABC中,∠ACB=90°,![]() ,则:
,则:![]() .
.
(1)解决问题:
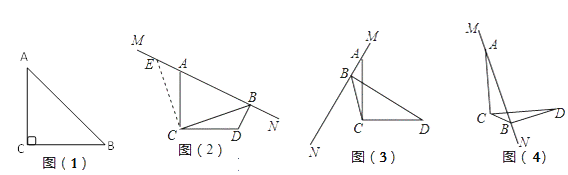
如图(2),∠ACD = 90°,AC = DC,MN是过点A的直线,过点D作DB⊥MN于点B,连接CB,试探究线段BA、BC、BD之间的数量关系.
不妨过点C作CE⊥CB,与MN交于点E,易发现图中出现了一对全等三角形,即 ≌ ,由此可得线段BA、BC、BD之间的数量关系是: .
(2)类比探究:
将图(2)中的MN绕点A旋转到图(3)的位置,其它条件不变,试探究线段BA、BC、BD之间的数量关系,并证明.
(3)拓展应用:
将图(2)中的MN绕点A旋转到图(4)的位置,其它条件不变,若BD=2,BC=![]() ,则AB的长为 .
,则AB的长为 .
【答案】(1)![]() ;(2) BD—AB=
;(2) BD—AB=![]() BC,理由详见解析;(3)4.
BC,理由详见解析;(3)4.
【解析】
(1)利用ASA证得![]() ,所以AE=BD,EB=AE+AB=BD+AB∵
,所以AE=BD,EB=AE+AB=BD+AB∵![]() ∴
∴![]()
(2)过点C作CE⊥CB, 与MN交于点E,利用ASA证得△ACE≌△DCB,进而求得线段之间的关系,同(1),即可证出.
(3)过点C作EC⊥CB交MN于点E,同(2),可证:![]() ,即可求出AB的长.
,即可求出AB的长.
(1)![]()
![]()
(2) BD—AB=![]() BC .
BC .
过点C作CE⊥CB, 与MN交于点E,则∠ECB=90°
∴∠ECB+∠BCA=∠ACD+∠BCA,即:∠ECA=∠BCD.
∵DB⊥MN, ∴∠ABD=∠ACD=90°,
记AC与BD的交点为点F,则∠BFA=∠DFC, ∴∠BAF=∠FDC
在△ACE与△DCB中,
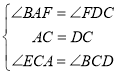
∴△ACE≌△DCB(ASA)
∴AE=BD, CE=CB
∴在Rt△BCE中, BE=![]() BC,
BC,
∴BD =AE=BA+BE= BA+![]() BC
BC
即BD—AB=![]() BC .
BC .
(3)
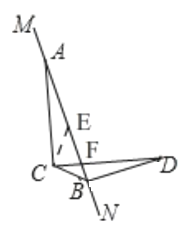
如图所示,过点C作EC⊥CB交MN于点E
同(2),可证:![]()
∴AE=BD=2
![]()
![]()


科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形网格中,点A,B,C均落在格点上.
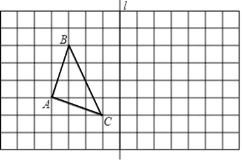
(1)直接写出△ABC的面积 .
(2)画出△ABC关于直线![]() 的轴对称图形△A1B1C1.
的轴对称图形△A1B1C1.
(3)判断△A1B1C1的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
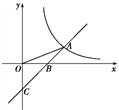
【题目】如图,已知直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数y=![]() 的图象在第一象限交于点A,连接OA,若S△AOB∶S△BOC=1∶2,则k的值为____.
的图象在第一象限交于点A,连接OA,若S△AOB∶S△BOC=1∶2,则k的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在一次环保知识宣传活动中,需要印刷若干份调查问卷。印刷厂有甲、乙两种收费方式:甲种方式收制版费6元,每一份收印刷费0.1元;乙种方式不收制版费,每印一份收印刷费0.12元。设共印调查问卷![]() 份:
份:
(1)按甲种方式应收费多少元,按乙种方式应收费多少元(用含![]() 的代数式表示);
的代数式表示);
(2)若共需印刷500份调查问卷,通过计算说明选用哪种方式合算?
(3)印刷多少份调查问卷时,甲、乙两种方式收费一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y=![]() (x>0)的图像经过点D,P是一次函数y=kx+3-3k(k≠0)的图像与该反比例函数图像的一个公共点.
(x>0)的图像经过点D,P是一次函数y=kx+3-3k(k≠0)的图像与该反比例函数图像的一个公共点.
(1)求反比例函数的表达式;
(2)通过计算说明一次函数y=kx+3-3k(k≠0)的图像一定经过点C;
(3)对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
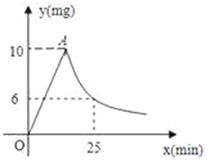
【题目】由于天气炎热,某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在_______分钟内,师生不能呆在教室.
查看答案和解析>>
科目:初中数学 来源: 题型:
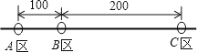
【题目】某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C,区有10人,三个区在一直线上,位置如图所示,公司的接送车打算在此间只设一个停靠点,为要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在_____区.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com