练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图1，中，，是的中点，平分交于点，在的延长线上且．

    （1）求证：四边形是平行四边形；

    （2）如图2若四边形是菱形，连接，，与交于点，连接，在不添加任何辅助线的情况下，请直接写出图2中的所有等边三角形．

    【答案】（1）详见解析；（2）△ACF、、、

    【解析】

    （1）在中，，是的中点，可得，再通过，得证，再通过证明，得证，即可证明四边形BCEF是平行四边形；

    （2）根据题意，直接写出符合条件的所有等边三角形即可．

    （1）证明：∵在中，，是的中点

    ∴，

    ∵，

    ∴，

    ∵平分，

    ∴，

    ∵，

    ∴，

    ∵，

    ∴，

    ∴

    又∵，

    ∴四边形BCEF是平行四边形；

    （2）∵四边形是菱形

    ∴，

    ∵

    ∴

    ∴△BCE和△BEF是等边三角形

    ∴

    ∴

    ∵

    ∴

    ∴

    ∴

    ∴

    ∴在△CDE和△CGE中

    ∴

    ∴

    ∴是等边三角形

    ∴

    ∴

    ∴

    ∴

    ∴

    ∴△ACF是等边三角形

    ∴等边三角形有△ACF，，，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一商店销售某种商品，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件．

    （1）若降价a元，则平均每天销售数量为 件．（用含a的代数式表示）

    （2）当每件商品降价多少元时，该商店每天销售利润为1200元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况（尺寸范围为176mm～185mm的产品为合格），随机各抽取了20个样品进行检测，过程如下：

    收集数据：（单位：mm）

    甲车间：168，175，180，185，172，189，185，182，185，174，192，180，185，178，173，185，169，187，176，180

    乙车间：186，180，189，183，176，173，178，167，180，175，178，182，180，179，185，180，184，182，180，183

    整理数据：

    频数

    组别

    165.5～170.5

    170.5～175.5

    175.5～180.5

    180.5～185.5

    185.5～190.5

    190.5～195.5

    甲车间

    2

    4

    5

    6

    2

    1

    乙车间

    1

    2

    a

    6

    2

    0

    分析数据：

    车间

    平均数

    众数

    中位数

    方差

    甲车间

    180

    185

    180

    43.1

    乙车间

    180

    180

    180

    22.6

    应用数据：

    （1）计算甲车间样品的合格率；

    （2）估计乙车间生产的8000个该款新产品中合格产品有多少个？

    （3）结合上述数据信息，请判断哪个车间生产的新产品更好，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四位同学在研究函数y=x2+bx+c(b，c是常数)时，甲发现当x=1时，函数有最小值；乙发现﹣1是方程x2+bx+c=0的一个根；丙发现函数的最小值为3；丁发现当x=2时，y=4，已知这四位同学中只有一位发现的结论是错误的，则该同学是( )

    A. 甲 B. 乙 C. 丙 D. 丁

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是的直径，点在上，，FD切于点，连接并延长交于点，点为中点，连接并延长交于点，连接，交于点，连接．

    （1）求证：；

    （2）若的半径为，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，点分别在边上，沿所在的直线折叠，使点的对应点恰好落在边上，若和相似，则的长为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，反比例函数图象在第一象限的分支上有一点C（1，3），过点C的直线y = kx+b〔k< 0〕与x轴交于点A.

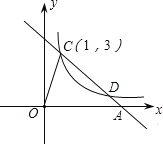
    （1）求反比例函数的解析式；

    （2）当直线与反比例函数的图象在第一象限内的另一交点的横坐标为3时，求△COD的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在Rt△ABC和Rt△ACD中，AC=BC，∠ACB=90°，∠ADC=90°，CD=2，(点A、B分别在直线CD的左右两侧)，射线CD交边AB于点E，点G是Rt△ABC的重心，射线CG交边AB于点F，AD=x，CE=y.

    (1)求证：∠DAB=∠DCF.

    (2)当点E在边CD上时，求y关于x的函数关系式，并写出x的取值范围.

    (3)如果△CDG是以CG为腰的等腰三角形，试求AD的长.

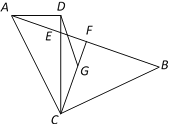
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)如图 1，若 P是口ABCD 边 CD 上任意一点，连结 AP、BP，若△APB 的面积为 60 ，△APD 的面积为 18，则 S△APC= .

    (2) 如图 2，①若点 P 运动到口ABCD 内一点时，试说明 S△APB +S△DPC =S△BPC +S△APD.

    ②若此时△APB 的面积为 60，△APD 的面积为 18，则 S△APC= .

    （3）如图 3①利用（2）中的方法你会发现，S△APB ，S△DPC ，S△BPC ，S△APD 之间存在怎样的关系： .

    ②若此时△APB 的面积为 60，△APD 的面积为 18，请利用你的发现，求 S△APC 的面积？

    查看答案和解析>>

    同步练习册答案