
【题目】如图,已知l1⊥l2 , ⊙O与l1 , l2都相切,⊙O的半径为2cm,矩形ABCD的边AD、AB分别与l1 , l2重合,AB=4 ![]() cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s)
cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s) 
(1)如图①,连接OA、AC,则∠OAC的度数为°;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1 , A1 , C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<2时,求t的取值范围(解答时可以利用备用图画出相关示意图).
【答案】
(1)105
(2)解:如图位置二,当O1,A1,C1恰好在同一直线上时,设⊙O1与l1的切点为E,
连接O1E,可得O1E=2,O1E⊥l1,
在Rt△A1D1C1中,∵A1D1=4,C1D1=4 ![]() ,
,
∴tan∠C1A1D1= ![]() ,∴∠C1A1D1=60°,
,∴∠C1A1D1=60°,
在Rt△A1O1E中,∠O1A1E=∠C1A1D1=60°,
∴A1E= ![]() =
= ![]() ,
,
∵A1E=AA1﹣OO1﹣2=t﹣2,
∴t﹣2= ![]() ,
,
∴t= ![]() +2,
+2,
∴OO1=3t=2 ![]() +6
+6
(3)解:①当直线AC与⊙O第一次相切时,设移动时间为t1,
如图位置一,此时⊙O移动到⊙O2的位置,矩形ABCD移动到A2B2C2D2的位置,
设⊙O2与直线l1,A2C2分别相切于点F,G,连接O2F,O2G,O2A2,
∴O2F⊥l1,O2G⊥A2C2,
由(2)得,∠C2A2D2=60°,∴∠GA2F=120°,
∴∠O2A2F=60°,
在Rt△A2O2F中,O2F=2,∴A2F= ![]() ,
,
∵OO2=3t1,AF=AA2+A2F=4t1+ ![]() ,
,
∴4t1+ ![]() ﹣3t1=2,
﹣3t1=2,
∴t1=2﹣ ![]() ,
,
②当直线AC与⊙O第二次相切时,设移动时间为t2,
记第一次相切时为位置一,点O1,A1,C1共线时位置二,第二次相切时为位置三,
由题意知,从位置一到位置二所用时间与位置二到位置三所用时间相等,
∴ ![]() +2﹣(2﹣
+2﹣(2﹣ ![]() )=t2﹣(
)=t2﹣( ![]() +2),
+2),
解得:t2=2+2 ![]() ,
,
综上所述,当d<2时,t的取值范围是:2﹣ ![]() <t<2+2
<t<2+2 ![]()
【解析】解:(1)∵l1⊥l2 , ⊙O与l1 , l2都相切,∴∠OAD=45°,
∵AB=4 ![]() cm,AD=4cm,
cm,AD=4cm,
∴CD=4 ![]() cm,
cm,
∴tan∠DAC= ![]() =
= ![]() =
= ![]() ,
,
∴∠DAC=60°,
∴∠OAC的度数为:∠OAD+∠DAC=105°,
所以答案是:105;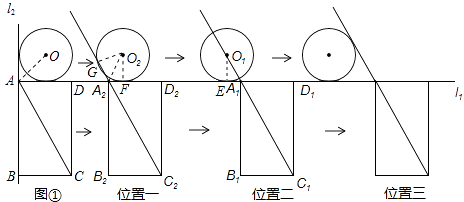


科目:初中数学 来源: 题型:
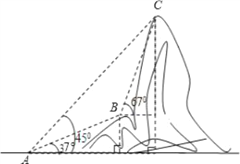
【题目】如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?
(精确到米,参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin67°≈
,sin67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
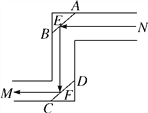
【题目】如图,潜望镜中的两个镜片AB和CD是平行的,光线经过镜子反射时,∠AEN=∠BEF,∠EFD=∠CFM,那么进入潜望镜的光线NE和离开潜望镜的光线FM是平行的吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.
(1)判断:一个内角为120°的菱形 等距四边形.(填“是”或“不是”)
(2)如图,在5×5的网格图中有A、B两点,请在答题卷给出的两个网格图上各找出C、D两个格点,使得以A、B、C、D为顶点的四边形为互不全等的“等距四边形”,画出相应的“等距四边形”,并写出该等距四边形的端点均为非等距点的对角线长.


端点均为非等距点的对角线长为 端点均为非等距点的对角线长为
(3)如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连结AD,AC ,BC,若四边形ABCD是以A为等距点的等距四边形,求∠BCD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC≌△DEF,A与D,B与E分别是对应顶点,∠A=52°,∠B=67°,BC=15cm,则∠F=________,FE=_________cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com