
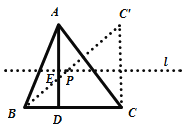
【题目】如图,△ABC中,AD垂直BC于点D,且AD=BC,BC上方有一动点P满足![]() ,则点P到B、C两点距离之和最小时,∠PBC的度数为( )
,则点P到B、C两点距离之和最小时,∠PBC的度数为( )

A.30°B.45°C.60°D.90°
【答案】B
【解析】
根据![]() 得出点P到BC的距离等于AD的一半,即点P在过AD的中点且平行于BC的直线l上,则此问题转化成在直线l上求作一点P,使得点P到B、C两点距离之和最小,作出点C关于直线l的对称点C’,连接BC’,然后根据条件证明△BCC’是等腰直角三角形即可得出∠PBC的度数.
得出点P到BC的距离等于AD的一半,即点P在过AD的中点且平行于BC的直线l上,则此问题转化成在直线l上求作一点P,使得点P到B、C两点距离之和最小,作出点C关于直线l的对称点C’,连接BC’,然后根据条件证明△BCC’是等腰直角三角形即可得出∠PBC的度数.
解:∵![]() ,
,
∴点P到BC的距离=![]() AD,
AD,
∴点P在过AD的中点E且平行于BC的直线l上,
作C点关于直线l的对称点C’,连接BC’,交直线l于点P,
则点P即为到B、C两点距离之和最小的点,
∵AD⊥BC,E为AD的中点,l∥BC,点C和点C’关于直线l对称,
∴CC’=AD=BC,CC’⊥BC,
∴三角形BCC’是等腰直角三角形,
∴∠PBC=45°.
故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() .
.

(1)在图中画出![]() ,
,![]() 的面积是_____________;
的面积是_____________;
(2)若点![]() 与点
与点![]() 关于
关于![]() 轴对称,则点
轴对称,则点![]() 的坐标为_____________;
的坐标为_____________;
(3)已知![]() 为
为![]() 轴上一点,若
轴上一点,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)在图中的点上标出相应字母A、B、C,并求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的边OA与x轴重合,B的坐标为(﹣1,2),将矩形OABC绕平面内一点P顺时针旋转90°,使A、C两点恰好落在反比例函数![]() 的图象上,则旋转中心P点的坐标是( )
的图象上,则旋转中心P点的坐标是( )

A. (![]() ,﹣
,﹣![]() ) B. (
) B. (![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,﹣
,﹣![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“唱红歌”比赛活动,八年级1、2班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.

(1)根据统计图所给的信息填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
八(1) | 85 | _____ | 85 |
八(2) | _____ | 80 | _____ |
(2)若八(1)班复赛成绩的方差s12=70,请计算八(2)班复赛成绩的方差s22,并说明哪个班级5名选手的复赛成绩更平稳一些.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段BC=8,射线CG⊥BC,A为射线CG上一点,已知FA⊥AB且FA=AB,AE平分∠FAB,且E点满足∠EBA=∠ABC.

(1)求证:△ABE≌△AFE.
(2)证明:FD⊥BC.
(3)求△BED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是在写字台上放置一本摊开的数学书和一个折叠式台灯时的截面示意图,已知摊开的数学书AB长20cm,台灯上半节DE长40cm,下半节DC长50cm.当台灯灯泡E恰好在数学书AB的中点O的正上方时,台灯上、下半节的夹角即∠EDC=120°,下半节DC与写字台FG的夹角即∠DCG=75°,求BC的长.(书的厚度和台灯底座的宽度、高度都忽略不计,F、A、O、B、C、G在同一条直线上.参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.41,结果精确到0.1)
≈1.41,结果精确到0.1)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com