
【题目】某自行车行销售甲、乙两种品牌的自行车,若购进甲品牌自行车5辆,乙品牌自行车6辆,需要进货款9500元,若购进甲品牌自行车3辆,乙品牌自行车2辆,需要进货款4500元.
(1)求甲、乙两种品牌自行车每辆进货价分别为多少元;
(2)今年夏天,车行决定购进甲、乙两种品牌自行车共50辆,在销售过程中,甲品牌自行车的利润率为![]() ,乙品牌自行车的利润率为
,乙品牌自行车的利润率为![]() ,若将所购进的自行车全部销售完毕后其利润不少于29500,那么此次最多购进多少辆乙种品牌自行车?
,若将所购进的自行车全部销售完毕后其利润不少于29500,那么此次最多购进多少辆乙种品牌自行车?
【答案】(1)甲种品牌自行车每辆进货价为1000元,乙种品牌自行车每辆进货价为750元;(2)此次最多购进30辆乙种品牌自行车.
【解析】
(1)设甲种品牌自行车每辆进货价为x元,乙种品牌自行车每辆进货价为y元,根据“购进甲品牌自行车5辆,乙品牌自行车6辆,需要进货款9500元;购进甲品牌自行车3辆,乙品牌自行车2辆,需要进货款4500元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购进乙种品牌自行车m辆,则购进甲种品牌自行车(50-m)辆,根据利润=成本×利润率,即可得出关于m的一元一次不等式,解之取其中的最大值即可得出结论.
解:(1)设甲种品牌自行车每辆进货价为x元,乙种品牌自行车每辆进货价为y元,
依题意,得:![]() ,
,
解得:![]() .
.
答:甲种品牌自行车每辆进货价为1000元,乙种品牌自行车每辆进货价为750元.
(2)设购进乙种品牌自行车m辆,则购进甲种品牌自行车(50-m)辆,
依题意,得:1000×(50-m)×80%+750m×60%≥29500,
解得:m≤30.
答:此次最多购进30辆乙种品牌自行车.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OC=2OB则下列结论:①abc<0;②a+b+c>0;③ac﹣2b+4=0;④OAOB=![]() ,其中正确的结论有( )
,其中正确的结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宝鸡市某学校在“行读石鼓阁”研学活动中,参观了我市中华石鼓园,石鼓阁是宝鸡城市新地标.建筑面积7200平方米,为我国西北第一高阁.小亮想知道石鼓阁的高是多少,他和同学小明对石鼓阁进行测量.测量方案如下:如图,小明在小亮和“石鼓阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小明看着镜面上的标记,他来回走动,走到点D时,看到“石鼓阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小明眼睛与地面的高度ED=1.6米,CD=2.2米,然后,在阳光下,小亮从D点沿DM方向走了29.6米,此时“石鼓阁”影子与小亮的影子顶端恰好重合,测得小亮身高1.6米,影长FH=3.2米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“石鼓阁”的高AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
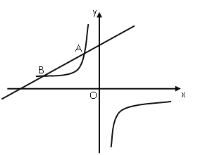
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OC2=OA·OB.

(1)证明:tan∠BAC· tan∠ABC=1;
(2)若点C的坐标为(0,2),tan∠OCB=2,
①求该抛物线的表达式;
②若点D是该抛物线上的一点,且位于直线BC上方,当四边形ABDC的面积最大时,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com