
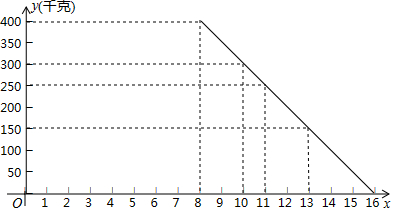
分析 (1)根据图象中点的坐标,利用待定系数法即可求出y与x的函数关系式;
(2)根据总利润=每千克销售利润×销售数量,即可得出W关于x的函数关系式,再利用配方法结合二次函数的性质,即可解决最值问题;
(3)由销售成本不超过2200元,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,再令W=600,通过解一元二次方程即可得出x的值,此题得解.
解答 解:(1)设y与x的函数关系式为y=kx+b(k≠0),
将(10,300)、(11,250)代入y=kx+b中,
$\left\{\begin{array}{l}{10k+b=300}\\{11k+b=250}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-50}\\{b=800}\end{array}\right.$,
∴y与x的函数关系式为y=-50x+800(8≤x≤16).
(2)根据题意得:W=(x-8)•y=(x-8)(-50x+800)=-50x2+1200x-6400.
∵W=-50(x-12)2+800,
∴当x=12时,W取最大值,最大值为800.
(3)根据题意得:8y=-400x+6400≤2200,
解得:x≥$\frac{21}{2}$.
令W=-50x2+1200x-6400=600,
解得:x=14或x=10(舍去).
∴商店想在销售成本不超过2200元的情况下,使销售利润达到600,销售单价应定为14元.
点评 本题考查了二次函数的应用、待定系数法求一次函数解析式、二次函数的性质、解一元一次不等式以及解一元二次方程,解题的关键是:(1)根据图象上点的坐标,利用待定系数求出函数关系式;(2)根据数量关系,找出W关于x的函数关系式;(3)通过解一元一次不等式及一元二次方程找出销售单价.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
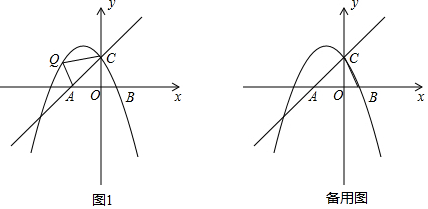
 如图,点A的坐标为(-8,0),点P的坐标为$({-\frac{7}{4},0})$,直线y=$\frac{3}{4}$x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
如图,点A的坐标为(-8,0),点P的坐标为$({-\frac{7}{4},0})$,直线y=$\frac{3}{4}$x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
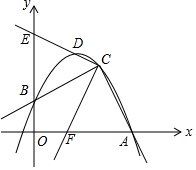 如图,已知二次函数y=ax2+bx+c的图象经过A(3,0),B(0,1),C(2,2)三点.
如图,已知二次函数y=ax2+bx+c的图象经过A(3,0),B(0,1),C(2,2)三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
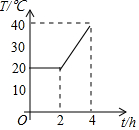 一个试验室在0:00-4:00的温度T(单位:℃)与时间t (单位:h)的函数关系的图象如图所示,在0:00-2:00保持恒温,在2:00-4:00匀速升温,则开始升温后试验室每小时升高的温度为( )
一个试验室在0:00-4:00的温度T(单位:℃)与时间t (单位:h)的函数关系的图象如图所示,在0:00-2:00保持恒温,在2:00-4:00匀速升温,则开始升温后试验室每小时升高的温度为( )| A. | 5℃ | B. | 10℃ | C. | 20℃ | D. | 40℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com