
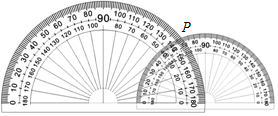
 如图,小量角器的0°刻度线在大量角器的0°刻度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在大量角器上对应的度数为40°,那么在小量角器上对应的度数为70°.(只考虑小于90°的角度)
如图,小量角器的0°刻度线在大量角器的0°刻度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在大量角器上对应的度数为40°,那么在小量角器上对应的度数为70°.(只考虑小于90°的角度)  金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3+a2=a5 | B. | (-a3b2)2=a6b4 | C. | 2x2÷2x2=0 | D. | (-$\frac{1}{2}$)-3=8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
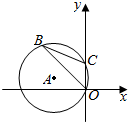 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上的一点,则cos∠OBC=( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上的一点,则cos∠OBC=( )| A. | $\frac{1}{3}$ | B. | 2$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 两组对角分别相等的四边形是平行四边形 | |
| C. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| D. | 对角线相等的平行四边形是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
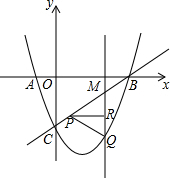 如图,抛物线y=ax2-(a+1)x-3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.
如图,抛物线y=ax2-(a+1)x-3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com