
【题目】“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
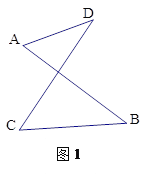
已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题:
问题一:在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系 ;
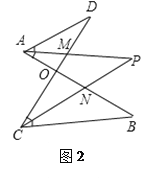
问题二:在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,试求∠P的度数;
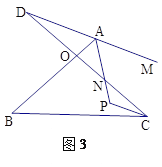
问题三:在图3中,已知AP、CP分别平分∠BAM、∠BCD,请问∠P与∠B、∠D之间存在着怎样的数量关系?并说明理由.
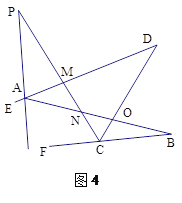
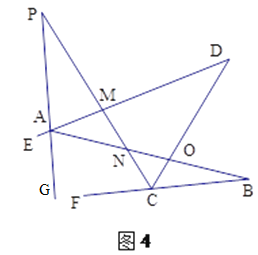
问题四:在图4中,已知AP的反向延长线平分∠EAB,CP平分∠DCF,请直接写出∠P与∠B、∠D之间的数量关系 .
【答案】(1)![]() (2)38°(3)
(2)38°(3)![]() (4)
(4) ![]()
【解析】分析:(1)利用三角形的内角和定理表示出∠AOD与∠BOC,再根据对顶角相等可得∠AOD=∠BOC,然后整理即可得解;
(2)根据(1)的关系式求出∠OCB﹣∠OAD,再根据角平分线的定义求出∠DAM﹣∠PCM,然后利用“8字形”的关系式列式整理即可得解;
(3)根据“8字形”数量关系有:∠P+∠PCN=∠D+∠DAN=∠D+180°-∠MAN①,∠B+2∠PCN=∠D+180°-2∠MAN②,由①和②即可得到结论;
(4)根据“8字形”数量关系有:∠P+∠PAN=∠B+∠BCN,∠D+∠DAN=∠B+∠BCO,即∠P+180°-∠GAN=∠B+180°-∠FCN①,∠D+180°-2∠GAN =∠B+180°-2∠FCN②,由①②可得结论.
详解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D.在△BOC中,∠BOC=180°﹣∠B﹣∠C.
∵∠AOD=∠BOC(对顶角相等),∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,∴∠A+∠D=∠B+∠C;
(2)∵∠D=40°,∠B=36°,∴∠OAD+40°=∠OCB+36°,∴∠OCB﹣∠OAD=4°.
∵AP、CP分别是∠DAB和∠BCD的角平分线,∴∠DAM=![]() ∠OAD,∠PCM=
∠OAD,∠PCM=![]() ∠OCB.
∠OCB.
又∵∠DAM+∠D=∠PCM+∠P,∴∠P=∠DAM+∠D﹣∠PCM=![]() (∠OAD﹣∠OCB)+∠D=
(∠OAD﹣∠OCB)+∠D=![]() ×(﹣4°)+40°=38°;
×(﹣4°)+40°=38°;
(3)根据“8字形”数量关系有:∠P+∠PCN=∠D+∠DAN=∠D+180°-∠MAN①,∠B+∠BCN=∠D+∠DAO=∠D+180°-∠MAB,∴∠B+2∠PCN=∠D+180°-2∠MAN②,由①和②得:∠D+∠B=2∠P-180°;
(4)根据“8字形”数量关系有:∠P+∠PAN=∠B+∠BCN,∠D+∠DAN=∠B+∠BCO,
∴∠P+180°-∠
由①②得:2∠P-∠B=∠D.


科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),B→C( , ),C→ (+1, );
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出P的位置;

(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(4)若图中另有两个格点M、N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
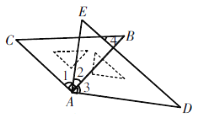
【题目】将一副三角板按如图放置,则下列结论:
①如果∠2=30°,则有AC∥DE;
②∠BAE+∠CAD =180°;
③如果BC∥AD,则有∠2=45°;
④如果∠CAD=150°,必有∠4=∠C;
正确的有( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=42°,∠DAE=18°.
(1)若设∠DAC=x°,则∠BAC= °,∠C= °;(用含x的代数式表示)
(2)求∠C的度数;
(3)请直接写出∠AEC与∠B、∠C之间的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将一块腰长为 ![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
(1)点A的坐标为 , 点B的坐标为;
(2)抛物线的解析式为;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a>0)的顶点为P,其图像与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:
①m=3;
②当∠APB=120°时,a= ![]() ;
;
③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;
④抛物线上存在点N,当△ABN为直角三角形时,有a≥ ![]()
正确的是( )
A.①②
B.③④
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)△ABC中任意一点M(a,b)经过平移后的对应点为M′(a+2,b+1),将△ABC作同样的平移,得到△A′B′C′,写出A′、B′、C′的坐标,并在图中画出平移后图形.
(2)求出三角形ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com