
分析 先通分,再利用平方差公式和二次根式的性质与法则化简,最后计算分式的减法,代入求值即可.
解答 解:原式=$\frac{{\sqrt{x}(\sqrt{x}+\sqrt{y})}}{{(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})}}-\frac{{\sqrt{y}(\sqrt{x}-\sqrt{y})}}{{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}}$
=$\frac{{x+\sqrt{xy}}}{x-y}-\frac{{\sqrt{xy}-y}}{x-y}$
=$\frac{x+y}{x-y}$,
当x=3,y=2时,
原式=$\frac{x+y}{x-y}=\frac{3+2}{3-2}=5$.
点评 本题主要考查分式的化简求值与二次根式的化简求值,熟练掌握分式与二次根式的运算法则与性质是解题的关键.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:选择题
 如果表示a,b两个数的点在数轴上的位置如图所示,那么化简式子$\sqrt{(a-b)^{2}}$-|a|+$\sqrt{{b}^{2}}$的结果等于( )
如果表示a,b两个数的点在数轴上的位置如图所示,那么化简式子$\sqrt{(a-b)^{2}}$-|a|+$\sqrt{{b}^{2}}$的结果等于( )| A. | 0 | B. | 2a | C. | 2b | D. | 2a-2b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
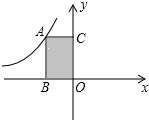 如图,矩形ABOC的面积为$\sqrt{2}$,反比例函数y=$\frac{k}{x}$的图象过点A,则k的值为( )
如图,矩形ABOC的面积为$\sqrt{2}$,反比例函数y=$\frac{k}{x}$的图象过点A,则k的值为( )| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com