

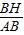 ≈0.56,即可计算出AB的长;而AC=BD=1m,从而得到所用不锈钢材料的总长度l=AC+AB+BD;
≈0.56,即可计算出AB的长;而AC=BD=1m,从而得到所用不锈钢材料的总长度l=AC+AB+BD;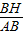 ≈0.56,计算出AH,即得到EM;
≈0.56,计算出AH,即得到EM;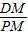 ,计算出AM,然后由PE=PM-EM=AM-AH得到PE的长度.
,计算出AM,然后由PE=PM-EM=AM-AH得到PE的长度.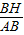 ≈0.56,即AB=
≈0.56,即AB= ≈3.21(m),
≈3.21(m),
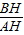 =0.68,
=0.68, ≈2.65(m),
≈2.65(m),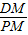 ,
,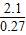 ≈7.78m,
≈7.78m,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2011年广东省深圳市宝安区中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年广东省深圳市宝安区中考数学一模试卷(解析版) 题型:选择题
 (x-2)2-2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2,过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
(x-2)2-2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2,过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
 (x-2)2+4
(x-2)2+4 (x-2)2+3
(x-2)2+3 (x-2)2+2
(x-2)2+2 (x-2)2+1
(x-2)2+1查看答案和解析>>
科目:初中数学 来源:2011年广东省深圳市宝安区中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011年广东省深圳市宝安区中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年广东省深圳市宝安区中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com