练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
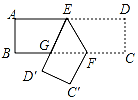
    20．把一张长方形纸片按图中那样折叠后，若得到∠BGD′=40°，则∠C′FE=110°．

    分析 先根据图形折叠的性质求出∠DEF的度数，再由平行线的性质即可得出结论．

    解答 解：∵AD∥BC，
    ∴∠BGD′=∠AEG=40°，
    由折叠的性质得，∠DEF=∠D′EF=$\frac{1}{2}$（180°-40°）=70°，
    ∴∠C′FE=∠EFC=180°-∠E=DEF=110°
    故答案为：110．

    点评 本题考查了平行线的性质：两直线平行，内错角相等；两直线平行，同旁内角互补；两直线平行，同位角相等．也考查了折叠的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示，点P在y=$\frac{k}{x}$的图象上，PC⊥x轴于点C，交y=$\frac{1}{x}$的图象于点A，PD⊥y轴于点D，交y=$\frac{1}{x}$的图象于点B．当点P在y=$\frac{k}{x}$的图象上运动时，以下结论：
    ①S△ODB=S△OCA
    ②S四边形PAOB的值不会发生变化
    ③PA与PB始终相等
    ④当点A是PC的中点时，点B一定是PD的中点．
    其中一定不正确的是（　　）
    A．①B．②C．③D．④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知：在矩形ABCD中，AB=8，BC=12，四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上，AE=2．
    （1）如图1，当四边形EFGH为正方形时，求△GFC的面积；
    （2）如图2，当四边形EFGH为菱形时，设BF=x，△GFC的面积为S，求S关于x的函数关系式，并写出函数的定义域．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．在（ax+3y）与（x-y）的积中，不含有xy项，则a=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知：如图，∠1=∠C，∠3=∠4，求证：∠2=∠D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图1，已知AB∥CD，∠B=30°，∠D=120°；
    （1）若∠E=60°，则∠F=90°；
    （2）请探索∠E与∠F之间满足的数量关系？说明理由；
    （3）如图2，已知EP平分∠BEF，FG平分∠EFD，反向延长FG交EP于点P，求∠P的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．阅读并补充下面推理过程：（1）如图1，已知点A是BC外一点，连接AB，AC．求∠BAC+∠B+∠C的度数．
    解：过点A作ED∥BC，所以∠B=∠EAD，∠C=∠DAE．
    又因为∠EAB+∠BAC+∠DAC=180°．
    所以∠B+∠BAC+∠C=180°．
    方法运用：（2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数．
    深化拓展：（3）已知AB∥CD，点C在点D的右侧，∠ADC=70°，BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间．
    ?．如图3，点B在点A的左侧，若∠ABC=60°，则∠BED的度数为65°．
    Ⅱ．如图4，点B在点A的右侧，且AB＜CD，AD＜BC．若∠ABC=n°，则∠BED的度数为215°-$\frac{1}{2}$n°．（用含n的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．某校为美化校园，计划对面积为1800平方米区域进行绿化，安排甲、乙两个工程队完成．已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400平方米区域绿化时，甲队比乙队少用4天．求甲、乙两工程队每天能完成绿化的面积分别是多少平方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

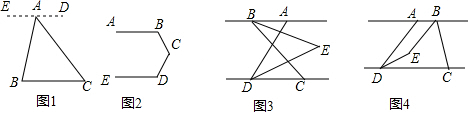
    10．如图，直线DE与直线AB、CD分别交于点E、D、EG平分∠DEB，直线GF与直线AB交于点F，若∠CDE=116°，∠AFG=130°，∠G=8°．判断直线AB、CD是否平行？并说明理由．

    查看答案和解析>>

    同步练习册答案