
分析 (1)先设未知数:单独完成这个路段的施工任务乙工程队需x天,甲工程队需$\frac{2}{3}$x天,则甲工程队的工效为:$\frac{1}{\frac{2x}{3}}$,乙工程队的工效为:$\frac{1}{x}$,根据甲施工10天,剩下的工程再由甲、乙两个工程队合作施工30天完成列方程即可解出;
(2)求设未知数求出乙工程队还需做45天完成,再设乙工程队每天施工的费用为a万元,根据施工费用共计211.5万元,列方程得出结论;
(3)先根据总工作量÷总工效=总工作时间,计算出需合作36天完成,再根据(2)中的一天的费用:3+2.5=5.5万元,计算需总费用198万元,所以不够用,需补18万元.
解答 解:(1)设乙工程队单独完成这个路段的施工任务需x天,则甲工程队单独完成这个路段的施工任务需$\frac{2}{3}$x天,
根据题意得:$\frac{10}{\frac{2x}{3}}$+$\frac{30}{\frac{2x}{3}}$+$\frac{30}{x}$=1,
解得:x=90,
经检验:x=90是原方程的解,
当x=90时,$\frac{2}{3}$x=$\frac{2}{3}$×90=60,
答:甲、乙工程队单独完成这个路段的施工任务各需60天、90天;
(2)由(1)得:甲工程队的工效:$\frac{1}{60}$,乙工程队的工效为:$\frac{1}{90}$,
设甲、乙两个工程队共同施工18天后,再由乙工程队单独做还需y天完成剩下的施工任务,
则$\frac{18}{60}+\frac{18}{90}+\frac{y}{90}$=1,
解得:y=45,
经检验:x=45是原方程的解,
∴甲一共做了18天,乙一共做了18+45=63天,
设乙工程队每天施工的费用为a万元,则甲工程队每天施工的费用为1.2a万元,
则18×1.2a+63a=211.5,
84.6a=211.5,
a=2.5,
1.2a=1.2×2.5=3,
答:甲工程队每天施工的费用为3万元;
(3)若由甲、乙工程队合作完成,则所需时间为:1÷($\frac{1}{60}$+$\frac{1}{90}$)=36(天)
36×(2.5+3)=198>180,
198-180=18,
答:工程预算费用不够用,需追加预算18万元.
点评 本题考查了分式方程的应用,属于工程问题;明确三个量的关系:总工作量、工作效率、工作时间,熟记总工作量=工作效率×工作时间;列分式方程解应用题一定要审清题意,找相等关系是着眼点,要学会分析题意,提高理解能力,并注意方程要检验.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
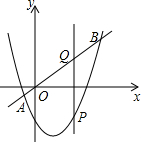 如图所示,直线y=x与抛物线 y=x2-x-3交于A,B两点,点P是抛物线上的一个动点,点P作PQ⊥x轴交直线y=x于点Q,设点P的横坐标为m,则线段PQ的长度随着m的增大而减小时m的取值范围是m<-1或1<m<3.
如图所示,直线y=x与抛物线 y=x2-x-3交于A,B两点,点P是抛物线上的一个动点,点P作PQ⊥x轴交直线y=x于点Q,设点P的横坐标为m,则线段PQ的长度随着m的增大而减小时m的取值范围是m<-1或1<m<3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
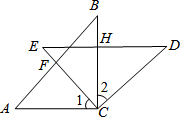 如图,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.
如图,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com