
 定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形.
定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形.分析 (1)由折叠即可得到DG=GH=CH;
(2)只需借鉴阅读中证明“四边形BCEF为$\sqrt{2}$矩形”的方法就可解决问题;
(3)同(2)中的证明可得:将$\sqrt{3}$矩形沿用(2)中的方式操作1次后,得到一个“$\sqrt{4}$矩形”,将$\sqrt{4}$矩形沿用(2)中的方式操作1次后,得到一个“$\sqrt{5}$矩形”,将$\sqrt{5}$矩形沿用(2)中的方式操作1次后,得到一个“$\sqrt{6}$矩形”,由此就可得到n的值.
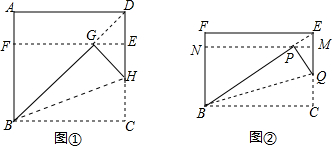
解答 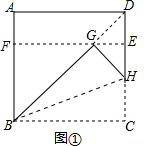 解:(1)如图①,由折叠可得:
解:(1)如图①,由折叠可得:
DG=HG,GH=CH,
∴DG=GH=CH.
故答案为:GH、DG;
(2)如图②,∵BC=1,EC=BF=$\frac{\sqrt{2}}{2}$,
∴BE=$\sqrt{E{C}^{2}+B{C}^{2}}$=$\frac{\sqrt{6}}{2}$.
由折叠可得BP=BC=1,∠FNM=∠BNM=90°,∠EMN=∠CMN=90°.
∵四边形BCEF是矩形,
∴∠F=∠FEC=∠C=∠FBC=90°,
∴四边形BCMN是矩形,∠BNM=∠F=90°,
∴MN∥EF,
∴$\frac{BP}{BE}$=$\frac{BN}{BF}$,即BP•BF=BE•BN,
∴1×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}}{2}$BN,
∴BN=$\frac{1}{\sqrt{3}}$,
∴BC:BN=1:$\frac{1}{\sqrt{3}}$=$\sqrt{3}$:1,
∴四边形BCMN是$\sqrt{3}$的矩形;
(3)同理可得:
将$\sqrt{3}$矩形沿用(2)中的方式操作1次后,得到一个“$\sqrt{4}$矩形”,
将$\sqrt{4}$矩形沿用(2)中的方式操作1次后,得到一个“$\sqrt{5}$矩形”,
将$\sqrt{5}$矩形沿用(2)中的方式操作1次后,得到一个“$\sqrt{6}$矩形”,
所以将图②中的$\sqrt{3}$矩形BCMN沿用(2)中的方式操作3次后,得到一个“$\sqrt{6}$矩形”,
故答案为6.
点评 本题综合考查了轴对称的性质、正方形的性质、矩形的判定与性质、平行线分线段成比例、勾股定理等知识,考查了阅读理解能力、操作能力、归纳探究能力、推理能力,运用已有经验解决问题的能力,是一道好题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| z(元/m2) | 50 | 52 | 54 | 56 | 58 | … |
| x(年) | 1 | 2 | 3 | 4 | 5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
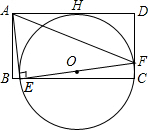 如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,∠AFE=30°,△ECF的外接圆切AD于H,则sin∠DAF=$\frac{3}{14}\sqrt{3}$.
如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,∠AFE=30°,△ECF的外接圆切AD于H,则sin∠DAF=$\frac{3}{14}\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
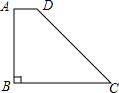 在梯形ABCD中,AD∥BC,∠ABC=90°,AB=CB,tan∠C=$\frac{4}{3}$(如图),点E在CD边上运动,联结BE.如果EC=EB,那么$\frac{DE}{CD}$的值是$\frac{1}{3}$.
在梯形ABCD中,AD∥BC,∠ABC=90°,AB=CB,tan∠C=$\frac{4}{3}$(如图),点E在CD边上运动,联结BE.如果EC=EB,那么$\frac{DE}{CD}$的值是$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 容量,方差 | B. | 平均数,容量 | C. | 容量,平均数 | D. | 离差,平均数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com