
���� ��1�����ò��������ʽ�ֽ⼴�ɣ�
��2�����ݲ��϶��ṩ�Ľ��ⲽ���뷽�����н��
��� �⣺��1��x4-7x2+9��
=x4-6x2+9-x2��
=��x2-3��2-x2��
=��x2-3+x����x2-3-x����
��2�����ʽ$\frac{4x-3}{��2x+1����x-2��}$=$\frac{m}{2x+1}$-$\frac{n}{x-2}$��
����ʽ���ұ�ͨ�ֵã�$\frac{m��x-2��-n��2x+1��}{��2x+1����x-2��}$=$\frac{��m-2n��x-��2m+n��}{��2x+1����x-2��}$��
��$\frac{4x-3}{��2x+1����x-2��}$=$\frac{��m-2n��x-��2m+n��}{��2x+1����x-2��}$��$\left\{\begin{array}{l}{m-2n=4}\\{2m+n=3}\end{array}\right.$��
���$\left\{\begin{array}{l}{m=2}\\{n=-1}\end{array}\right.$��
����$\frac{4x-3}{��2x+1����x-2��}$=$\frac{2}{2x+1}$+$\frac{1}{x-2}$��
���� ���⿼������ʽ�ֽ��Ӧ�ã���Ϥ�����ṩ�Ľ��ⷽ���Ͳ����ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
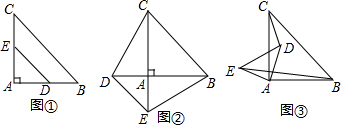
 ��ͼ����D��E�ֱ��ڡ�ABC��BC��AC�ϣ������߶�AD��BE���ڵ�F����AE��EC=1��3��BD��DC=2��3����EF��FB=$\frac{3}{8}$��
��ͼ����D��E�ֱ��ڡ�ABC��BC��AC�ϣ������߶�AD��BE���ڵ�F����AE��EC=1��3��BD��DC=2��3����EF��FB=$\frac{3}{8}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��6 | B�� | -1��x��6 | C�� | -1��x��6 | D�� | x��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 2 | C�� | 4 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com